ABSTRACT
This study presents a vertically deployable rotor-sail structure utilizing multi-layer Sarrus linkages. The structure fully extends during sailing to maximize Magnus lift and compresses to less than half its length for docking. An analytical beam model integrates link thickness, mid part spacing, and centrifugal loading to predict deflection and mass. Parametric comparisons of two-layer, six-layer, and twelve-layer configurations reveal that the twelve-layer design reduces structural mass by 90% while meeting an L/1000 deflection limit. Dynamic simulations using RecurDyn confirm that mid part segmentation decreases damping time and reduces peak stress, thus enhancing deployability and mechanical reliability. The findings offer quantitative design guidance for high-speed rotating deployable structures.
-
KEYWORDS: Deployable structure, Rotor sail, Sarrus linkage, Dynamic simulation
-
KEYWORDS: 전계형 구조, 회전 돛, Sarrus 링키지, 동역학 해석
1. 서론
지속 가능한 해양 운송 기술에 대한 관심이 전 세계적으로 증가하면서, 친환경적인 추진 방식에 대한 다양한 대안이 모색되고 있다[
1-
5]. 특히, 국제해사기구(International Maritime Organization, 이하 IMO)는 2023년 개정된 전략(2023 IMO Strategy on Reduction of GHG Emissions from Ships)을 통해, 2050년까지 국제 해운 부문의 온실가스 배출량을 감축하겠다는 목표를 제시하였다. 이 전략에는 2030년까지 전 선박의 탄소 집약도(Carbon Intensity)를 2008년 대비 최소 40% 감축, 2050년까지는 선박 전체에서 발생하는 GHG 배출을 가능한 한 조기에 완전 제거하는 중장기 로드맵이 포함되어 있다[
5]. 이러한 규제 강화 흐름 속에서 풍력을 이용한 보조 추진 장치는 기존 선박의 추진 에너지를 보조하여 연료 소비를 줄이고 탄소 배출을 저감할 수 있는 기술로 다시 주목받고 있다[
6-
17].
이 중에서도 Rotor Sail은 Magnus 효과를 기반으로 작동하는 장치로, 회전하는 원통형 구조물이 주변 유체 속도를 비대칭으로 유도하여 양력을 생성한다. 생성된 양력은 선박의 진행 방향에 따라 추진력을 제공하며, 특히 기존 추진 시스템에 병렬로 적용 가능하다는 점에서 높은 연비 효율성과 지속가능성을 갖는다. Rotor Sail은 이미 여러 대형 선박에 실증 적용된 바 있으며, 실제 해상 운항 환경에서 연료 소비 절감이 가능하다[
6,
18].
기존의 로터세일은 일반적으로 고정형으로 설치되기 때문에, 평상시 항해 외의 상황에서는 공간 간섭, 적재 효율 저하, 항만 접안 시의 물리적 제약 등 다양한 운용상의 문제를 야기한다. 특히 대형 구조물이 갑판 위에 상시 존재할 경우, 선박의 조타 유연성과 유지보수 접근성이 저하되는 문제가 발생할 수 있다. 반면, Rotor Sail은 구조물의 높이가 증가할수록 Magnus 효과에 따른 양력 생성 효율이 향상되는 특성을 가지며, 실제로 높이 30 m의 구조물은 하단부 대비 상단부에서 약 60% 더 빠른 유속을 받아 더 큰 양력을 생성한다[
19]. 이러한 특성은 추진 성능 향상 측면에서 유리하지만, 구조물이 지나치게 높아질 경우 교량 하부 통과나 항만 접안과 같은 항로 운항에서의 물리적 간섭을 초래할 수 있다. 결과적으로 시스템의 성능과 운용 유연성 간의 Trad e-off가 존재하며, 이를 기술적으로 해결하기 위한 전개형(Deployable) 구조 설계가 요구된다. 또한, 회전 운용 조건의 로터세일에서는 원심 하중이 지배적으로 적용하며, 전개 프레임의 처짐을 허용치 이내로 유지하기 위해 단면 두께 증대 등 강성 보강이 요구된다.
그러나 두께 증가는 구조 질량의 증가로 직결되고, 이는 지지 베어링에 전달되는 방사·축하중을 키워 마찰모멘트와 손실전력을 증가시켜 구동 효율을 저하시키는 요인으로 작용한다[
20]. 동시에 상부 갑판에 설치되는 장치의 질량이 커질수록 선박의 질량중심이 상승하여 선박 운행의 안전 측면에서 불리한 영향을 초래한다[
11].
이러한 이유로 로터세일 구조에는 처짐 억제와 경량화라는 상충하는 목표(Trade-off)를 동시에 달성할 수 있는 설계 전략이 요구된다. 본 연구는 Sarrus 링키지 기반의 다중 전개형 구조를 그 해결책으로 제안한다. Sarrus 링키지는 회전 관절만으로 순수 병진 운동을 유도할 수 있는 구조로, 구조 자체에 전개 경로가 내재되어 있어 구동 단순화와 기구학적 안정성을 동시에 제공한다.
특히, 이를
Figs. 1 과
2 같이 다중 형태로 설계하면, 각 층의 병진 운동이 하나의 구동 링키지에 의해 동기화될 수 있어, 단일 모터 구동만으로도 대형 구조물 전체의 제어가 가능해진다.
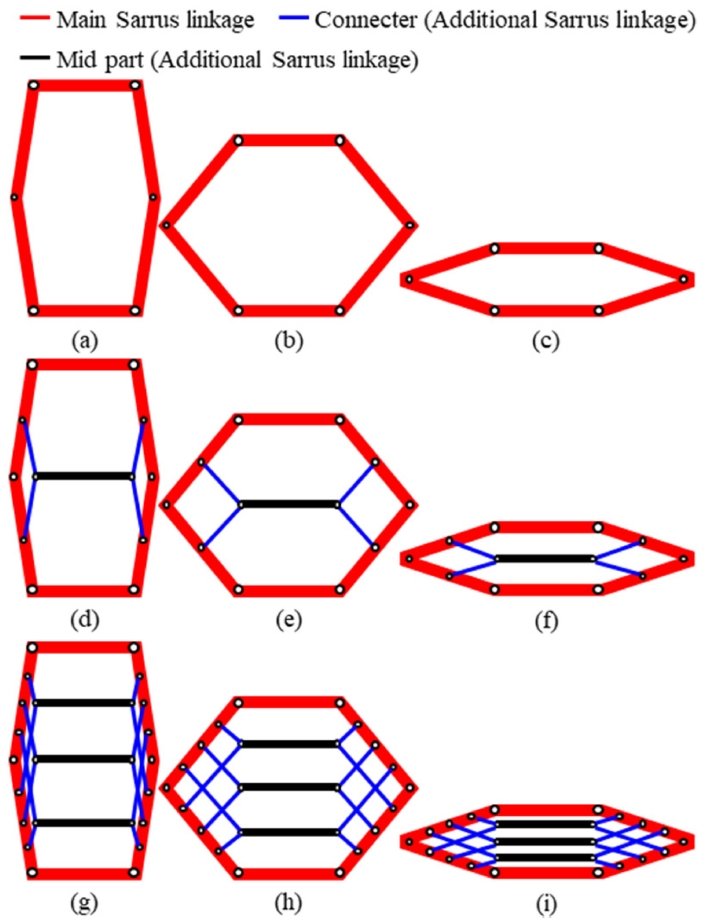
Figs. 2(a)-
2(c)는 기본 메인 Sarrus 링키지의 직선 전개 운동을 나타내며,
2(d)-
2(f)는 추가 링크 세트 1개를 부착한 이중 Sarrus 구조,
2(g)-
2(i)는 3세트를 부착한 삼중 구조를 나타낸다. 보조 링크 세트가 추가되더라도 메인 구조의 구동 경로에는 영향을 주지 않으며, 동일한 구동 입력으로 병진 운동이 유지된다. 단, 삼중 구조 이상에서는 커넥터 간의 간섭이 발생할 수 있으므로, 이들 커넥터 링크는 리지드 링크 대신 텐던(Tendon)으로 구성하여 간섭을 최소화하고, 구조의 직선 정렬성을 보조하도록 설계하였다.
본 연구는 이러한 구조적 설계를 기반으로, 다중 구조의 적용이 단순히 기구학적 확장성뿐만 아니라 구조 강성의 분산을 가능케 하며, 결과적으로 메인 Sarrus 링크의 두께를 감소시켜 전체 중량을 줄이는 효과가 있음을 수학적 모델과 해석을 통해 정량적으로 증명한다. 첫째, 로터세일을 위한 다중 Sarrus 링키지 구조의 설계 전략을 제시하고, 구조적 분할이 전체 전개 강성에 미치는 영향을 분석한다. 둘째, 단순 보 이론을 적용하여 각 구조물에 요구되는 최소 두께를 계산하고, 다중화에 따른 중량 최적화 가능성을 평가한다. 셋째, 동역학 시뮬레이션을 통해 설계 구조의 실제 강성 확보와 고속 회전 조건 하 동역학적 안정성을 검증한다. 이로써, 본 연구는 다중 Sarrus 구조가 기존 이중 구조 대비 구조 두께와 무게를 최대 90% 이상 경량화할 수 있음을 실증하고, 고회전 조건에서도 충분한 구조 강성과 정밀한 전개 성능을 유지할 수 있음을 입증한다.
2. 설계
Rotor Sail 시스템에 적용 가능한 접이식 구조물을 구현하기 위해, 본 연구에서는 다중 Sarrus 링키지를 활용한 전개형 구조 프레임을 제안한다. 해당 구조물은 항해 중에는 원통형 구조로 전개되고, 평상시 운항이나 항만 접안 시에는 수직 방향으로 압축되어 수납될 수 있도록 설계되었다. 전개 및 수납이 가능한 기구학적 구조를 통해 운항 조건에 따른 공간 활용의 유연성을 확보하는 데 초점을 두고 있다. 본 장에서는 이러한 구조적 목적을 달성하기 위한 메커니즘 설계의 구성 원리와 형상 조건, 소형 프로토타입 제작을 통한 구현 및 다중 Sarrus 링키지로의 확장 가능성 그리고 구조 해석에 필요한 설계 인자들을 단계적으로 기술한다.
2.1 이중 Sarrus 링키지의 기구학적 구조
Sarrus 링키지는 회전 조인트만으로 수직 방향의 병진 운동을 유도할 수 있는 평행 링크 메커니즘으로, 슬라이딩 부재 없이도 선형 운동을 구현할 수 있다[
21]. 최소 6개의 링크로 구성되며, 상하단 플레이트를 연결하는 메커니즘으로, 정렬된 링크들이 기하학적으로 제한된 경로를 따라 동기화되면서 전체 구조의 상단과 하단 사이에 직선 운동을 생성한다.
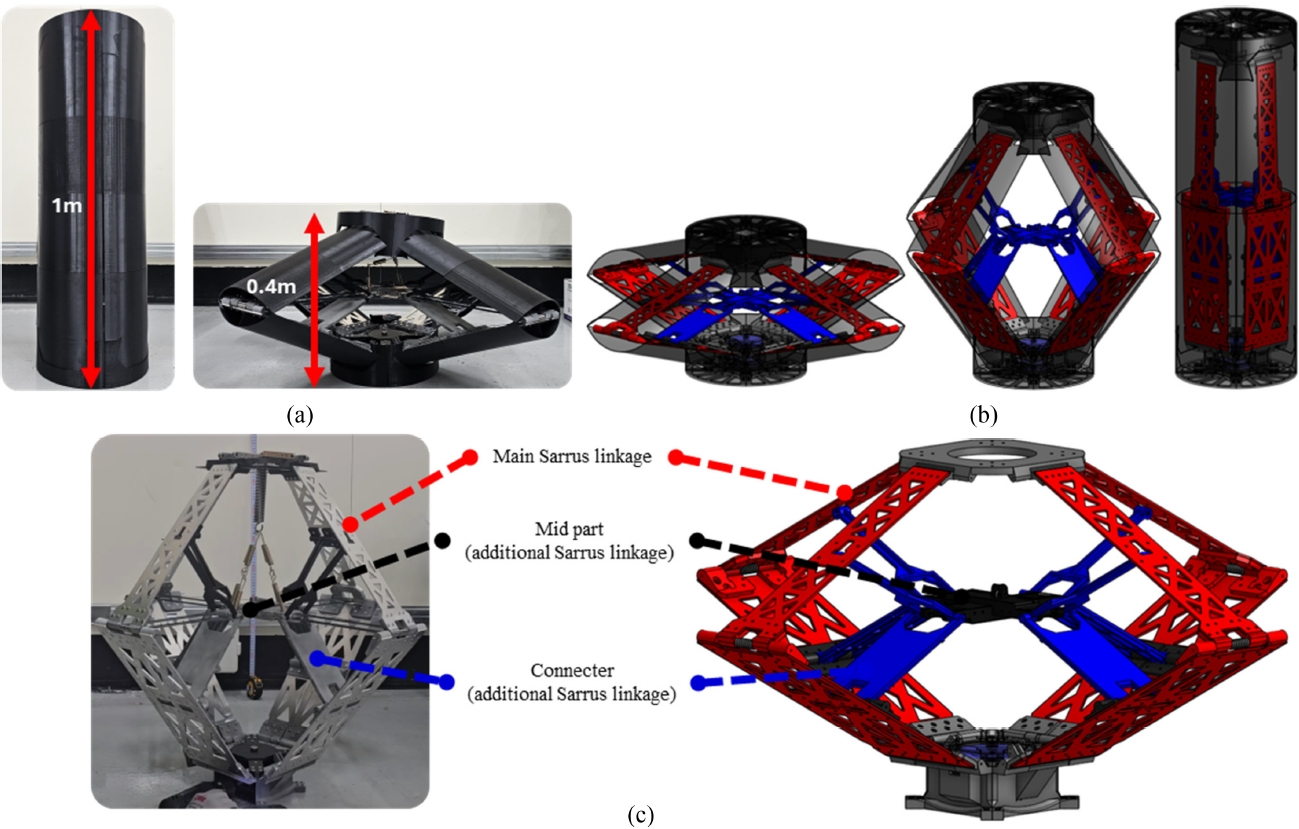
Fig. 1은 제안하는 다중 Sarrus 링키지 구조의 설계와 프로토 타입을 상세히 보여준다.
Fig. 1(a)는 1 : 15 스케일로 제작된 소형 프로토타입으로, 1m 높이로 전개된 상태와 0.4 m로 수납된 상태를 나타낸다.
Fig. 1(b)는 3D CAD 모델을 통해 접힌 상태에서 완전히 전개되기까지의 동기화된 전개 과정을 보여준다. 이 이중 Sarrus 링키지 프로토타입을 통해, 추가 링크(Additional Linkage)가 부착되어도 단일 Sarrus 링키지와 동일한 1자유도 직선 운동이 구현됨을 확인하였으며, 이는 다중 Sarrus 링키지로의 확장 가능성을 시사한다.
소형 프로토타입은 총 10개의 링크로 구성된 ‘Main Sarrus 링키지’(
Fig. 1(c), 빨간색)를 기반으로, 내부에 ‘Mid Part’(검은색)와 ‘Connecter’(파란색)로 구성된 9개의 추가 Sarrus 링크가 부착된 사각기둥 형태이다.
Fig. 1(c)는 이 내부 링키지 시스템의 상세 구조를 실제 프로토타입 사진과 3D 모델을 비교하여 명확히 보여준다. Mid Part는 원심력에 의한 메인 Sarrus 링크의 밴딩을 억제할 수 있도록 잠금이 이루어진다.
Fig. 1은 해당 구조의 1 : 15 스케일 소형 프로토타입 설계를 나타낸다. 메인 프레임을 구성하는 링크 길이는 L = 410 mm, 보조 링크는 l = 205 mm로 설정되었으며, 링크 간의 초기 회전각은 θ = 68
o 기준으로 설정되었다. 프로토타입은 전개 시 높이 H = 1,000 mm, 수납 시 최소 높이 h = 400 mm로 약 2.5 배의 전개율을 갖는다. 전개 시에는 정해진 경로를 따라 각 링크가 병진 이동하며, 상하단 구조물의 상대적인 위치가 직선 경로로 제어된다. 이 구조는 전개 시에도 위치 정밀도와 경로 일관성을 확보할 수 있도록 기하학적으로 제한되어 1자유도를 갖는다.
이 구조는 단일 Sarrus 링키지 뿐만 아니라,
Fig. 2와 같이 이중 또는 삼중 Sarrus 링키지로 확장 가능하다.
Figs. 2(a)-
2(c)는 기본 Sarrus 링크의 병진 운동을 나타내며,
2(d)-
2(f)는 추가 보조 링크 1세트가 부착된 이중 구조,
2(g)-
2(i)는 3세트 이상으로 구성된 삼중 구조를 나타낸다. 이때 모든 구조는 메인 구동부가 동일하게 유지되며, 보조 링크는 텐던을 통해 간섭 없이 연속적으로 확장될 수 있다.
링크 부재는 모두 2D 형태로 접힐 수 있도록 얇은 평판 구조로 형성되었으며, 각 링크는 조인트를 따라 회전하도록 설계되었다. 이를 통해 구조물 제작의 단순화, 중량 절감, 그리고 공간 활용성 향상을 달성하였다.
실제 구현은 1 : 15 스케일의 이중 Sarrus 링키지 구조로 진행되었으며, 전개 및 수납 시의 직선 운동 확인과 기구학적 정합성을 검증하였다. 동일한 치수 조건 하에서 아크릴 소재를 이용해 삼중 Sarrus 링키지 구조를 추가로 제작하여 다층 구조 시의 구동 동기화 가능성을 실험적으로 확인하였다. 반면, 5중 이상의 다층 구조에 대해서는 실제 시제품 제작은 수행하지 않고, 동역학 해석을 기반으로 한 구조 안정성 및 전개 경로의 기구학적 타당성을 분석하였다.
2.2 다중 Sarrus 링키지 위한 추가 링크 설계
기본 메커니즘인 10개의 Sarrus 링키지로 구성된 메인 프레임 외부에, 9개의 보조 링크를 갖는 추가 Sarrus 링키지 모듈을 병렬로 적층 배치하였다(
Fig. 2). 각 보조 모듈은 메인 구조와 기하학적으로 동일한 운동 특성을 갖도록 설계되었으며, 전체 시스템은 하나의 구동에 의해 동기화되어 전개, 수납 과정이 동시에 수행되도록 구성되었다.
이중 이상의 다중 구조에서는 각 링크의 전개 범위가 중첩되는 구간이 발생하며, 보조 링크의 수가 증가할수록 이러한 간섭 가능성도 비례하여 커지게 된다. 이를 방지하고 전체 시스템의 기구학적 간결성을 유지하기 위해, 본 구조에서는 다음과 같은 설계 전략을 도입하였다.
메인 Sarrus 링키지는 알루미늄 제작된 리지드 링크로 구성되어 밴딩(Banding) 시뮬레이션을 진행하였으며, 보조 링크 간 연결은 텐던(Tendon)을 활용하여 구조의 무게를 최소화하고, 구동 중 발생할 수 있는 링크 간 충돌 및 간섭을 효과적으로 회피하도록 하였다. 텐던은 상하단 간 위상 고정을 유지하고 전체 구조의 직진성을 보조한다. 이와 같은 설계를 통해, 다중 Sarrus 링키지 구조의 정렬 정확도를 향상시키고, 반복 동작 시의 운동 신뢰성을 확보함과 동시에 경량화를 실현하였다.
2.3 다중 Sarrus 링키지의 구조 해석
다중 Sarrus 링키지 구조의 구조적 신뢰성 확보를 위해, 본절에서는 1 : 1 스케일을 기준으로 구조물이 회전 중 받는 원심 하중에 의한 변형 거동을 해석적으로 분석하였다. 구조물은 알루미늄 합금을 주재료로 가정하였으며, 항해 중 회전 운동을 수행함에 따라 각 링크 부재는 일정한 회전 반경을 따라 지속적인 원심력을 받는다. 이때 발생하는 밴딩 변형은 전개형 구조의 직선 구동 특성에 직접적인 영향을 미치며, 기구학적 정밀도 저하 및 기하학적 간섭을 유발할 수 있다.
해석에서는 원심 가속도에 의한 하중을 주요 외력으로 설정하고, 중력에 의한 가속도는 상대적으로 작고 구조물 전체에 균일하게 작용한다는 점에서 무시 가능한 수준으로 간주하였다. 실제 선박의 항해 속도 및 회전 반경 조건에서 원심 가속도가 중력가속도 g = 9.81 m/s2 보다 1차원적으로 우세하다는 점은 해석의 주요 가정으로 작용한다. 따라서 이 해석의 목적은 구조적 처짐을 억제하기 위한 보강 부재(Middle Part)의 개수와 간격을 산정하고, 이를 통해 전체 구조의 전개 신뢰성을 확보하는 것이다.
구조 해석에는 다음과 같은 설계 조건은 밀도 ρ = 2700 kg/m3, 탄성계수 E = 6.9 × 1010 Pa을 적용하였으며, 메인 Sarrus 링크의 길이는 6.1 m, 단면 너비는 2.2 m로 설정하였다. 회전 반경은 1.658 m, 회전 속도는 180 rpm으로 가정하였고, 이에 따른 원심 가속도는 식(1)과 같이 계산된다.
이 원심 가속도에 의해 작용하는 선형 하중 q는 식(2)와 같이 계산된다.
여기서 t는 링크의 두께이며, 이 선형 하중에 대한 최대 처짐은 단순 지지보를 기준으로 식(3)으로 계산된다.
이때, 단면 2차 모멘트 I는 직사각형 단면에 대해
식(4)로 주어지며, b는 링크의 단면 폭이다. 구조 설계 기준에서 변형 허용치는 구조물 길이의 1/1000 수준으로 설정하였으며, 이는 기존 해양 구조물 설계 기준과 일부 건축 구조 기준에서 제시된 허용 처짐 한계 내로 설정되었다[23].
위의 식(3)과 식(5)를 비교함으로써 구조물의 링크 두께 t에 대한 설계 기준을 도출하고, 주어진 하중 조건 하에서 구조가 허용 처짐 이내에서 안정적으로 동작하는지를 평가할 수 있다. 이를 기반으로 본 연구에서는 다양한 두께에 따른 Mid Part 개수 변화와 전체 구조 중량을 수치적으로 도출하였으며, 그 결과는 제3장에서 기술된다.
3. 결과
본 장에서는 회전에 의해 발생하는 원심 하중 조건 하에서, 메인 Sarrus 링키지의 처짐을 억제하기 위한 Mid Part 간격, 필요 개수, 그리고 전체 구조 중량을 수치적으로 도출하고, 그 경향을 분석하였다. 설계 타당성의 1차 검증을 위해 본 해석은 탄성 선형 모델을 가정하였으며, 마찰, 조인트, 텐던 장력 등의 비선형 효과는 후속 연구에서 다룰 예정이다.
3.1 Main 링크 두께에 따른 Mid Part 개수 및 전체 중량
해석은 링크 두께 t를 설계 변수로 설정하고, 각 두께에 대응되는 Mid Part 간격 Lgap을 식(1)-식(5)를 바탕으로 식(6)과 같이 계산한 후, 그에 따른 개수 및 중량을 추정하는 방식으로 진행되었다.
계산된 Lgap을 기반으로, 각 메인 링크(길이 6.1 m)에 필요한 Mid Part 개수는 식(7)과 같이 산정된다.
전체 구조물 중량은 메인 구조물 8개와 Mid Part 개수에 따라 식(8)과 같이 추산된다.
Fig. 3는 이 계산을 통해 도출된 결과를 도시한 것으로, 각 두께에 따른 Mid Part 개수 및 전체 중량의 변화 경향을 보여준다.
3.2 다층 Sarrus 구조의 동역학 해석
Fig. 4에 제시한 변형 형상 스냅숏을 보면 M id Part 층수가 증가할수록 굽힘 곡률이 상단부에서 하부 전체로 균등 분포됨을 알 수 있다. 회전 운동 중 발생하는 원심력에 대한 다층 Sarrus 링키지의 거동을 평가하기 위하여 RecureDyn으로 동역학 해석을 수행하였다. 모든 모델은 총 길이 L = 6.1 m, 회전 속도 ω = 18.85 rad/s (180 rpm)을 공통으로 적용하였고, 링크 두께 t 와 Mid Part 간격
Lgap은 앞서 도출한 설계식을 따랐다. 분석 대상은 Mid Part가 각각 1개, 5개, 11개인 이중, 육중, 십이중 구조이며, 허용 변형 한계는
Lgap/1000 (6.1, 2, 1 mm)로 설정하였다.
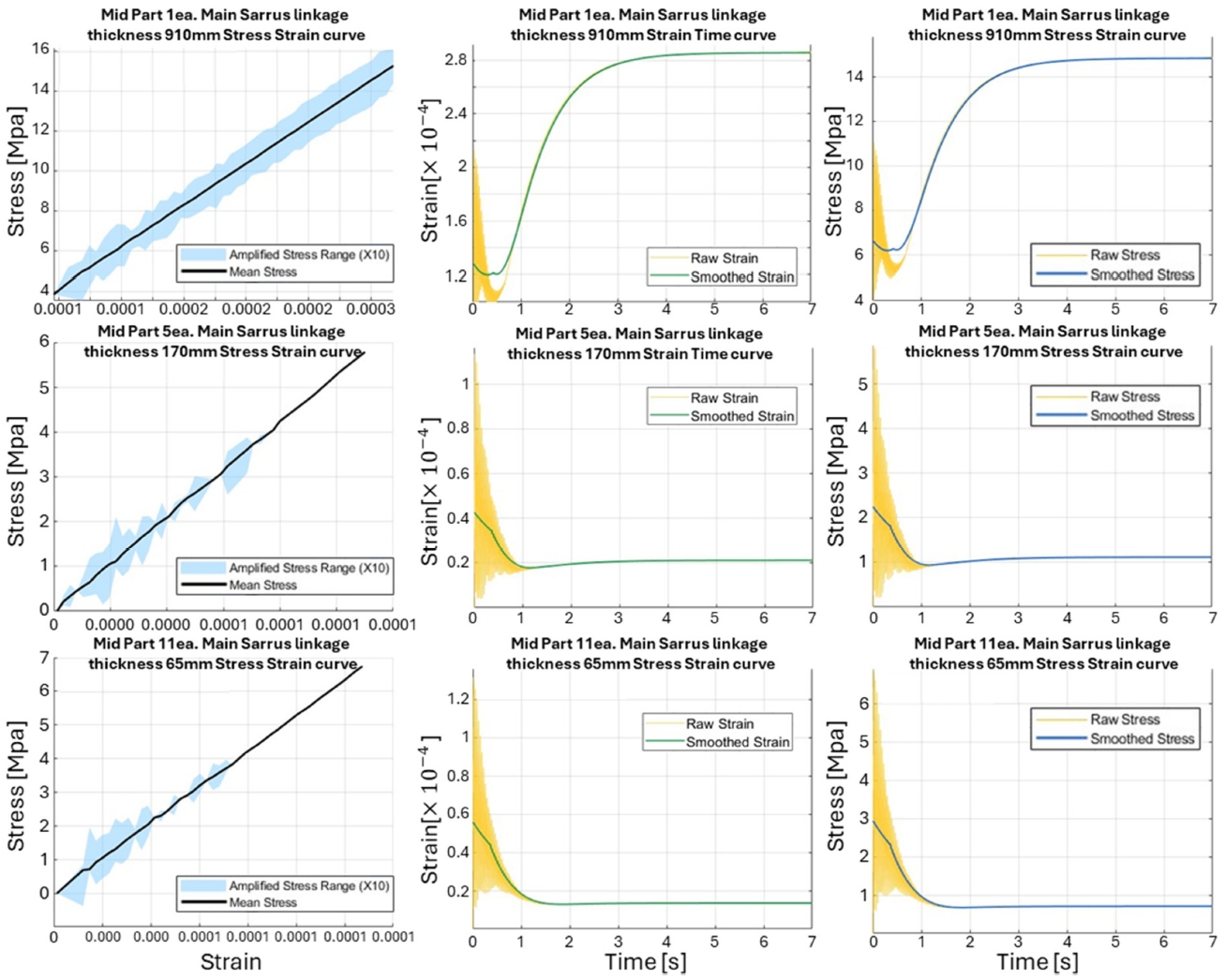
Fig. 5는 변형률 응력 시간을 조합한 곡선들을 제시한다. 세 구조 모두 동일한 각가속도를 받기 때문에 0-0.4 s 구간에서는 관성력이 지배적으로 작용하며, 이 구간에서 변위 변형률 응력이 동시에 급상승하는 특징이
Figs. 5(b) 및
5(c)에 공통적으로 나타난다. 이중 구조는 M id Part 수가 적어
Lgap이 상대적으로 크므로 관성력 지배 구간 이후에도 상대적으로 크게 휘어져 약 4 s 시점에 상단부 변위 4 mm, 변형률 400 με에 도달한다. 반면 육중 십이중 구조는 Mid Part 증가로 굽힘 강성이 향상되어 전체 처짐이 급격히 감소한다. 그 결과 정상 단계에서의 변형률과 응력은 각각 21 με/1.1 MPa(육중), 15 με/0.8 MPa(십이중) 수준으로 크게 낮아져 곡선이 시각적으로 완화되고 평탄해진다.
이중 구조의 경우 허용 처짐을 충족하기 위해 링크 두께가 약 910 mm에 달해 전체 중량이 262.5 t로 증가하지만, 육중 구조는 Mid Part 를 2.0 m 간격으로 배치함으로써 두께를 170 m, 중량을 51 t로 감소시킨다. 십이중 구조는 Mid Part 간격을 1.0 m로 더 촘촘히 하여 두께 65 mm 전체 중량은 19.5 t로 최소화되었다.
Fig. 5 전반을 종합하면 Mid Part 층수 증가에 따라 초기 가속 구간의 피크 이후 변형 응력이 급격히 감소함을 확인할 수 있다. 이는 다층화 전략이 원심 하중 조건에서도 구조 강성 향상과 중량 절감을 동시에 달성할 수 있음을 입증한다.
4. 결론
본 논문에서는 원통형 접이식 로터세일 구조물의 전개 및 수납을 위해, 다중 Sarrus 링키지 기반의 전개형 기구 프레임을 설계하고 해석하였다. 제안된 구조는 항해 중에는 전개 상태로 작동하고, 평상시에는 수직으로 압축되어 최소 부피로 수납될 수 있도록 고안되었다. 본 연구는 1자유도 기구 특성을 갖는 Sarrus 링키지를 다층 구조로 확장하여 직선 운동을 확보함으로써, 해양 구조물에 적용 가능한 실용적인 전개형 구조를 구현하는 것을 목표로 하였다.
이를 위해 1 : 15 스케일의 이중 Sarrus 링키지 소형 프로토 타입을 제작하였으며, 이후 동일 스케일에서 사중 구조의 구동 안정성까지 확인하였다. 오중 이상 구조는 실제 제작 없이 RecurDyn 기반의 동역학 시뮬레이션을 통해 검증하였으며, 링크 두께, 회전 반경, 회전 속도 등 다양한 조건을 바탕으로 원심 하중에 의한 구조적 변형을 해석적으로 예측하였다.
특히, Mid Part를 삽입하여 각 링크의 처짐을 제어하는 전략을 수립하였으며, 허용 변형 기준을 만족시키기 위한 Mid Part 간격과 개수를 설계 변수로 설정하여 전체 구조의 중량을 분석하였다. 분석 결과, 구조물의 중량을 20 ton 이하로 제한하면서도 허용 변형량을 만족시키기 위해서는 최소 11개의 M id Part 삽입이 필요하며, 이때 링크 두께는 약 65 mm로 설정되어야 함을 확인하였다.
향후 연구에서는 실제 스케일에 근접한 프로토타입을 통해 반복 동작 안정성과 해상 환경에서의 내구성 등을 종합적으로 검토할 계획이다. 본 연구의 동역학 해석 모델은 구조적 거동을 확인하기 위해 직사각형으로 단순화되었으나, 향후 실제 원통 형상에 가까운 곡면 모델을 적용하여 원심력의 영향을 더욱 정밀하게 분석하고, 이에 따른 최적의 링크 두께를 재검토할 것이다. 또한, 기존의 일체형 원통과 달리 본 구조는 분절된 형태이므로, 회전 시 발생할 수 있는 항력(Drag) 및 양력(Lift)의 변화 등 공기역학적 특성을 분석하기 위한 유체 역학(CFD) 해석이 추가로 필요하다. 이러한 분석을 바탕으로 향상된 전개력과 구조적 강성을 동시에 만족시키는 최적화 설계를 도출할 예정이며, 선박 시스템과의 통합성, 자동 전개 및 잠금 메커니즘 등의 후속 연구가 필요하다.
FOOTNOTES
-
ACKNOWLEDGEMENT
이 논문은 산업통상자원부의 재원으로 한국산업기술기획평가원(KEIT)의 지원을 받아 수행된 연구임(복합소재 풍력추진시스템 및 핵심부품 개발, No. 20024857).
Fig. 1Design and prototype of the multi-layer Sarrus deployable structure. (a) Small-scale (1 : 15) prototype shown deployed (1 m) and folded (0.4 m), (b) 3D CAD models illustrating the deployment sequence, and (c) Detailed view comparing the physical assembly and 3D model of the internal linkage, highlighting the Main Sarrus linkage (red), Mid part (black), and Connecter (blue)
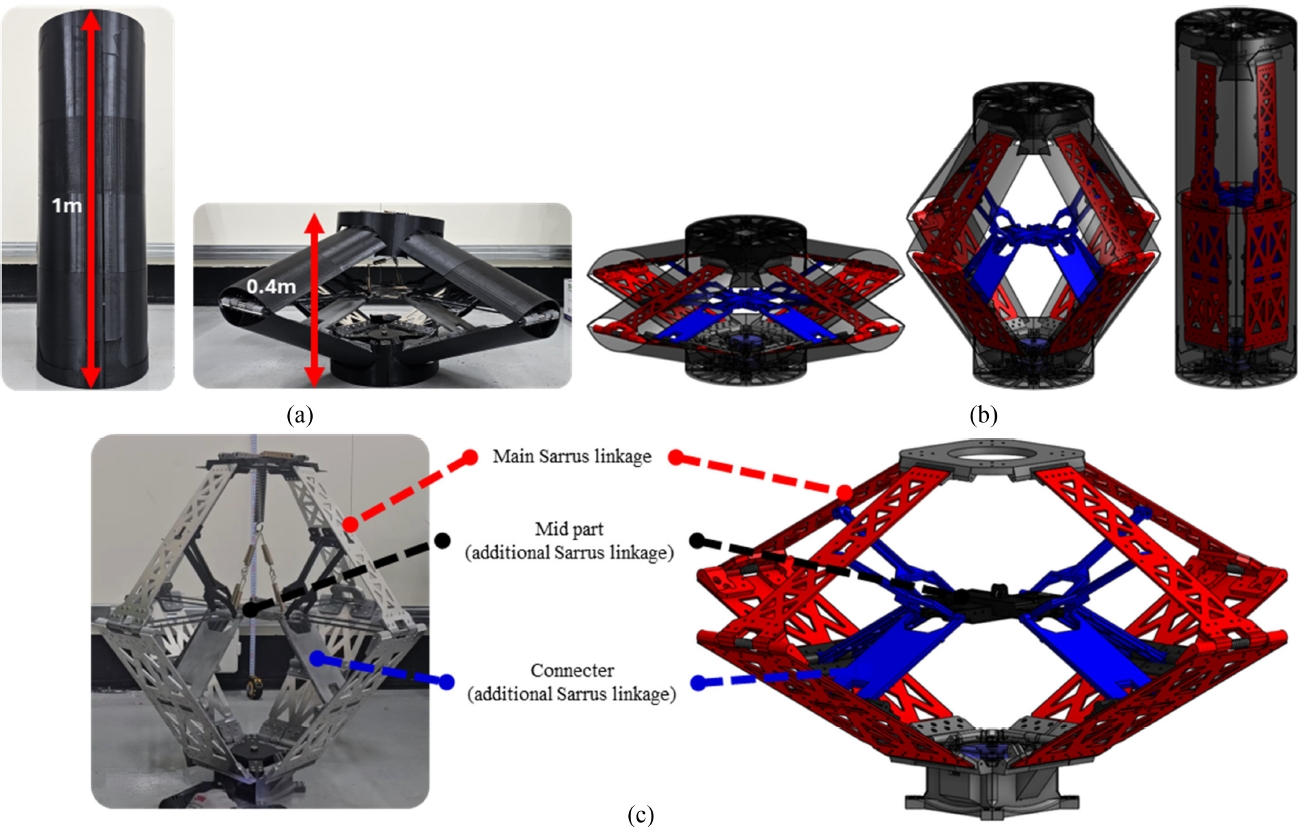
Fig. 2Sequential folding and deployment behavior of multilayer Sarrus linkages. (a)-(c) 1-layer (main Sarrus), (d)-(f) 2-layer (main + one auxiliary layer), and (g)-(i) 3-layer (main + two auxiliaries). The auxiliary layers do not interfere with the main linkage path and are synchronized by a single drive
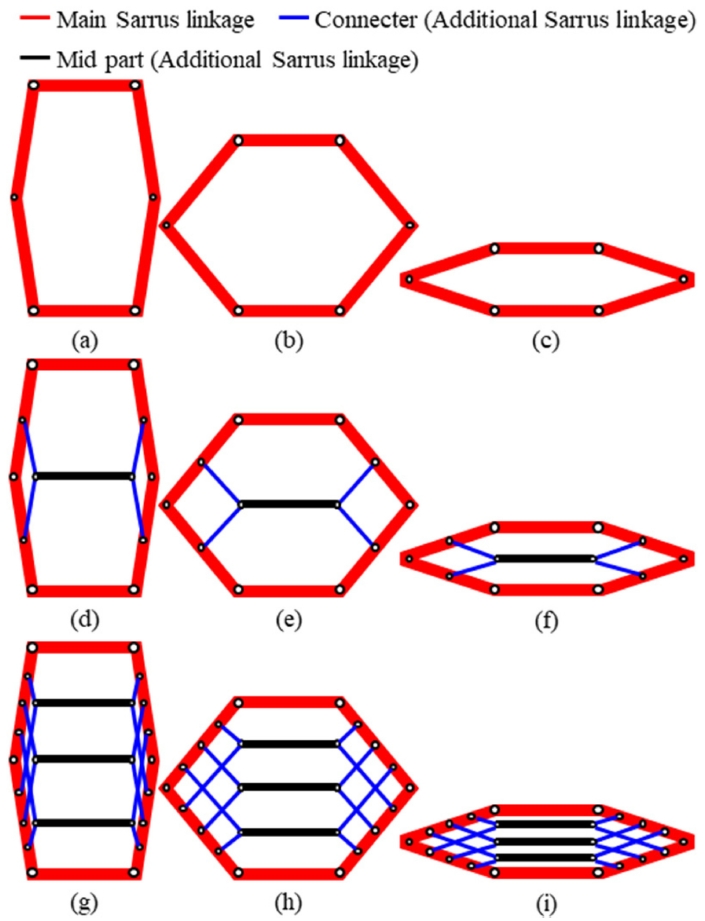
Fig. 3Structural weight analysis. The optimal design (red) satisfies the < 20 ton and ≤ 11 mid part goals with a 65 mm link thickness
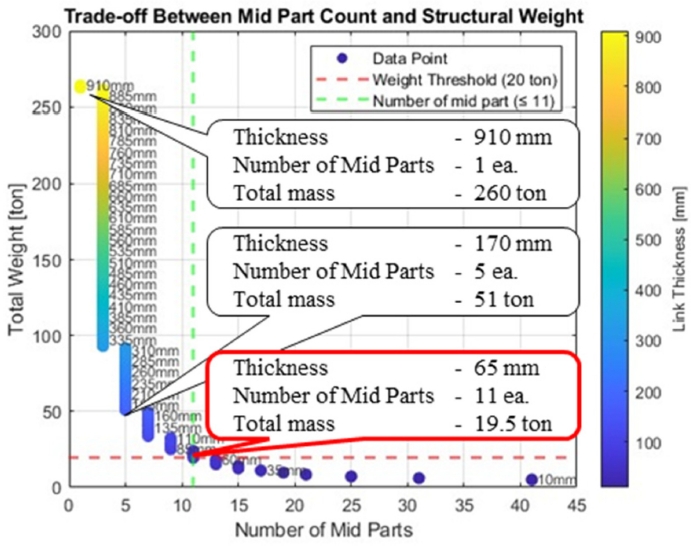
Fig. 4Dynamic analysis results of 2-layer, 5-layer, and 11-layer Sarrus structures under rotational speed of 18.85 rad/s. Each structure satisfies its target deformation criteria (6.1 mm, 2.0 mm, 1.0 mm), and structural stiffness increases with mid-part layering. Corresponding structural weights are 262.5 ton (2-layer), 51 ton (5-layer), and 19.5 ton (11-layer)

Fig. 5Dynamic response of multi-layer Sarrus linkages under centrifugal loading (ω = 18.85 rad / s). Rows correspond to mid-part counts of 1 (top, 2-layer), 5 (middle, 5-layer) and 11 (bottom, 11-layer); columns show (left) strain-averaged stress curve with 10 × amplified range band, (centre) time-history of strain with moving-average smoothing, and (right) time-history of stress with the same smoothing. Increasing the number of mid parts reduces peak strain and shortens the damping-to-steady-state interval
REFERENCES
- 1. Jeong, Y. K., Shin, J. G., Shen, H., Lee, P., and Woo, J. H., (2017), Calculation of green logistics KPI in shipbuilding process using shipyard logistics simulation, Proceedings of the Korean Society for Precision Engineering Spring Conference, 1095-1095.
- 2. Garg, C. P., Kashav, V., and Lam, J. S. L., (2025), Evaluation of value creating factors in green shipping corridors, Transportation Research Part D: Transport and Environment, 145, 104790.
- 3. Chen, S.-P., Li, J.-E., and Chen, Y.-X., (2025), Lifecycle cost-effectiveness analysis for greener alternative shipping fuels towards maritime energy sustainability, npj Clean Energy, 1(1), 6.
- 4. Duong, P. A., and Kang, H., (2025), Ammonia as fuel for marine dual-fuel technology: A comprehensive review, Fuel Processing Technology, 272, 108205.
- 5. Timas, A., and Mohammadi, M., (2025), Integrating weather-informed routing and energy optimization for sustainable maritime transportation, Ocean Engineering, 333, 121463.
- 6. Zhang, R., Huang, L., Wang, K., Ma, R., Ruan, Z., and Wang, C., (2024), Novel optimized layout for flettner rotors based on reuse of wake energy, Journal of Cleaner Production, 443, 140922.
- 7. Yeon, S., Kwon, C. S., Kim, Y.-C., Kim, K. S., Kim, Y. G., Kim, Y. H., and Kang, H. J., (2025), Performance analysis of flettner rotor considering marine wind profile and ship installation using CFD, International Journal of Naval Architecture and Ocean Engineering, 17, 100653.
- 8. Kolodziejski, M., and Sosnowski, M., (2025), Review of wind-assisted propulsion systems in maritime transport, Energies, 18(4), 897.
- 9. Carjova, K., Hilmola, O.-P., and Tapaninen, U., (2025), Economic feasibility and operational performance of rotor sails in maritime transport, Sustainability, 17(13), 5909.
- 10. Guzelbulut, C., Sugimoto, T., Fujita, Y., and Suzuki, K., (2024), Investigation of the efficiency of wind-assisted systems using model-based design approach, Journal of Marine Science and Technology, 29(2), 387-403.
- 11. Guzelbulut, C., and Suzuki, K., (2023), Optimal design of rotor sails based on environmental conditions and cost, Journal of marine science and engineering, 12(1), 31.
- 12. Yasuda, A., Taniguchi, T., and Katayama, T., (2024), Numerical investigation of aerodynamic interactions between rigid sails attached to ship, Journal of Marine Science and Engineering, 12(8), 1425.
- 13. Li, Z., and Tang, J., (2024), Circulation-controlled wind-assisted ship propulsion: Technical innovations for future shipping industry decarbonization, Energy Conversion and Management, 319, 118976.
- 14. Makram, T. E., Panagiotou, P., and Mattheou, D., (2023), Wingsail layout design and shape optimization using a CFD-aided taguchi approach: The aegean marathon case study, Ocean Engineering, 276, 114055.
- 15. Formosa, W., Sant, T., De Marco Muscat-Fenech, C., and Figari, M., (2023), Wind-assisted ship propulsion of a series 60 ship using a static kite sail, Journal of Marine Science and Engineering, 11(1), 117.
- 16. Chica, M., Hermann, R. R., and Lin, N., (2023), Adopting different wind-assisted ship propulsion technologies as fleet retrofit: An agent-based modeling approach, Technological Forecasting and Social Change, 192, 122559.
- 17. Talluri, L., Nalianda, D., Kyprianidis, K., Nikolaidis, T., and Pilidis, P., (2016), Techno economic and environmental assessment of wind assisted marine propulsion systems, Ocean Engineering, 121, 301-311.
- 18. Lee, K., Kim, Y. H., Park, J., Choi, B., and Kang, H. J., (2023), Preliminary feasibility study of a magnetic levitation rotor sail for coastal area operations, Journal of Marine Science and Engineering, 12(1), 32.
- 19. Tillig, F., and Ringsberg, J. W., (2020), Design, operation and analysis of wind-assisted cargo ships, Ocean Engineering, 211, 107603.
- 20. Kim, S.-J., Lee, D.-Y., Jung, G.-P., and Cho, K.-J., (2018), An origami-inspired, self-locking robotic arm that can be folded flat, Science Robotics, 3(16), eaar2915.
- 21. Okumoto Y., Takeda Y., Mano M., Okada T.. 2009. Design of ship hull structures: A practical guide for engineers. Springer Science & Business Media.
Biography
- Chan Kim
Ph.D. candidate in the Department of Mechanical Engineering, Seoul National University. His research interest is origami robotics.
- Sun-Pill Jung
Received the Ph.D. degree in the Department of Mechanical Engineering, Seoul National University. His research interest is origami robotics.
- JangGil Kim
Research professor in the SNU Engineering Consulting Center, Seoul National University. His research interest is Precision engineering, Structural mechanics.
- Kyu-Jin Cho
Professor in the Department of Mechanical Engineering, Seoul National University. His research interest is Bio-inspired, Soft robots.