ABSTRACT
In this study, we comparatively analyzed the convective heat transfer performance of single-wall and double-wall Gyroid TPMS (Triply Periodic Minimal Surface) structures. Using computational fluid dynamics (CFD), we evaluated the average convective heat transfer coefficients under constant surface temperature conditions for both constant velocity and constant pressure flow. Although both structures maintained the same fluid volume, the double-wall configuration increased the surface area by approximately 1.8 to 1.9 times, resulting in enhanced heat transfer performance. Under constant velocity conditions, the double-wall structure exhibited an average convective heat transfer coefficient that was 1.3 to 1.4 times higher than that of the single-wall structure. Under constant pressure conditions, we observed an increase of 1.06 to 1.1 times. Despite the double-wall structure leading to greater pressure losses due to increased shear stress from the formation of microchannels, it still maintained improved heat transfer performance even with reduced mass flow rates under constant pressure conditions. These findings provide fundamental data for designing TPMS-based cooling systems and optimizing additive manufacturing processes.
-
KEYWORDS: Triply periodic minimal surface, Gyroid structure, Convective heat transfer, Additive manufacturing, Energy balance
-
KEYWORDS: 삼중주기최소표면, 자이로이드 구조, 대류열전달, 적층 제조, 에너지 보존
NOMENCLATURE
Convection Heat Transfer Rate
Mean Convection Coefficient
Average Convection Coefficient
1. 서론
제조 산업은 오랜 기간 동안 절삭가공과 조형제조에 의존해 왔다. 절삭가공은 원재료에서 불필요한 부분을 제거하여 원하는 형상을 가공하는 방식으로 소재 낭비가 크며, 복잡한 형상 구현에 한계가 있다. 조형제조는 금형이나 주조 방식을 이용하여 제품을 성형하는 방식으로, 대량 생산에는 유리하지만 초기 금형 제작 비용이 높으며, 디자인 변경이 어렵다는 단점이 있다. 4차 산업혁명의 시점에서 제조 산업은 소재 활용도 향상, 복잡한 형상 구현, 맞춤형 생산 측면에서 적층제조(Additive Manufacturing, AM)가 주목받고 있다[
1,
2].
금속 적층제조에서는 PBF (Powder Bed Fusion)와 DED (Directed Energy Deposition), BJ ( Jetting) 방식등이 주로 활용되고 있으며, 비금속 적층제조에서는 FDM (Fused Deposition Modeling)과 SLA (Stereolithography) 방식등이 활용된다[
3]. 그러나 적층제조 기술 발전에도 불구하고 구조 설계 연구는 부진하다. 래티스 (Lattice)나 삼중주기최소표면(Triply Periodic Minimal Surface,TPMS) 연구는 단순 경량화를 넘어 일체화, 기능화, 최적화를 목표로 선행되어야 한다.
TPMS는 수학적으로 무한히 미분가능한 연속함수인 삼각함수의 조합으로 형성되는 구조이다. TPMS 구조에는 대표적으로 Gyroid, Diamond, Primitive가 있다[
4-
6]. 45
o 이하의 오버행이 발생할 때 서포트가 발생하지만 TPMS구조의 연속적 곡률은 오버행 각도를 완만하게 하여 서포트 생성을 최소화한다. 또한 3차원의 복잡한 구조이기 때문에 기존 절삭가공이나 조형제조로 구현하는 것보다 적층제조로 구현하는 것이 합당하며 경량화와 더불어 열전달 향상 등 기능적 측면에서 주목받고 있다. TPMS 구조는 주기, 위상을 조절함으로써 그 흐름을 변화시킬 수 있으며, 두께를 조절함으로써 유동속도를 조절하는 것도 가능하다. 최근 그 구조를 편리하게 구현할 수 있는 음함수 기반 상용 소프트웨어의 성능이 향상되면서 설계 자유도가 높아지고 있다[
7]. 특히 반도체 분야에서 웨이퍼에 새겨진 회로의 검사를 위한 프로브 스테이션의 하부척에 적용하여 온도균일도를 향상시킨 사례가 있다[
8,
9].
본 연구에서는 Gyroid를 사용한 두꺼운 T P MS에서 얇은 TPMS를 제거한 이중격벽 구조를 대상으로, 열전달 효율 측면에서 단일격벽 구조와의 성능 차이를 정량적으로 분석한다. 이를 위해 전산유체해석에서의 에너지 평형 검증을 수행하고, 일정 표면온도 조건에서 에너지 보존 법칙을 활용하여 평균 대류 열전달계수 산출 공식을 유도한다. 일정 유량 및 일정 압력에 대한 조건으로부터 평균 대류열전달계수를 계산해 단일격벽과 이중격벽 TPMS 구조의 성능을 비교한다.
2. 에너지 평형
2.1 에너지 보존
표면적 확장으로 인한 대류 열전달 성능 분석에 앞서 전산 유체해석의 신뢰성을 높이고자 에너지 보존에 관한 연구를 선행하였다. 단순화된 에너지 평형식은 식(1)와 같이 나타낼 수 있다[
10].
ṁ은 질량유량으로 비압축성유체라 가정하며, cp는 정압비열, Tin과 Tout은 입구와 출구의 온도를 의미한다. 비압축성 유체의 정상상태 조건하에서 식(1)은 항상 만족해야 한다.
식(1)의 경우 1차원으로 근사화하는 경우 입구와 출구온도는 한 점에서의 값이 되지만 3차원으로 근사화하는 경우 해당 단면적의 위치에 따라 그 값이 달라지므로 대푯값인 식(2)와 같은 평균 온도 Tm을 사용해야 한다.
따라서, 내부유동에서의 평균속도가 정의된 평균온도는 식(3)과 같이 나타낼 수 있다.
식(3)에서 이산화된 각 요소들의 속도와 온도, 면적으로부터 평균온도를 계산하면 식(4)와 같이 나타낼 수 있다. 즉 비압축성 유체이므로 밀도와 비열은 일정하다.
식(4)로부터 식(1)은 식(5)와 같이 나타낼 수 있다.
식(5)에서 Tm,o는 출구의 평균온도를 의미하며, Tm,i는 입구의 평균온도를 의미한다.
2.2 Newton의 냉각법칙
Newton의 냉각법칙은 식(6)과 같이 나타낼 수 있다.
여기서 h는 국소 대류열전달 계수이며, Ts는 표면온도를 의미한다. 또한 평균온도 Tm 내부유동에서 기준 온도로 활용하며, 이를 통해 열유속 qs′′를 계산할 수 있다. 이를 통해 열전달율은 열유속이 일정하거나 온도가 일정한 경우에 대해 수학적으로 계산할 수 있다.
2.3 일정 표면온도
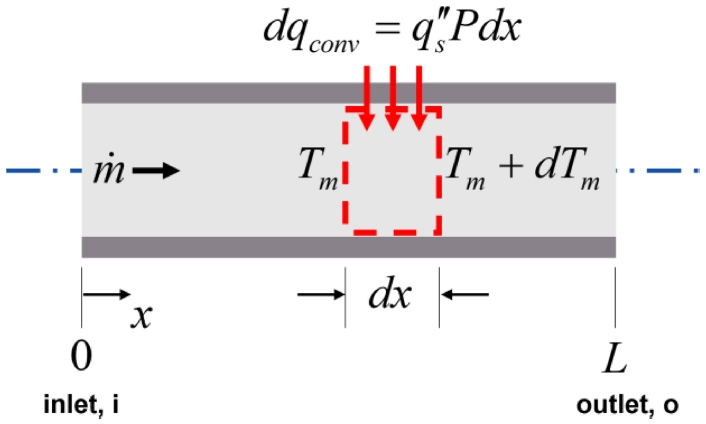
Fig. 1에서 보는 바와 같이 미소 검사체적에 대한 대류열전달율은 식(7)과 같이 나타낼 수 있다.
여기서 표면의 주변 길이 P를 도입하면 Pdqconv=qs′′Pdx와 같이 나타낼 수 있고, 식(7)에 식(6)을 대입하여 식(8)과 같이 나타낼 수 있다.
식(8)이 의미하는 바는 Ts>Tm인 경우 Tm은 x에 따라 증가하게 된다는 것이고, Ts<Tm인 경우 Tm은 x가 증가함에 따라 감소하게 된다는 것이다.
일정 표면온도에 대한 대류열전달계수를 파악하면 열전달의 성능을 파악할 수 있다. 이를 위해 식(8)의 Ts-Tm를 ∆T로 정의한다. 그러면 식(8)은 식(9)와 같이 나타낼 수 있다.
또한 변수분리를 통해 식(9)를 다시 정리하면 식(10)과 같이 나타낼 수 있다.
식(10)에서 좌항은 ∆Ti에서 ∆To까지, 우항은 입구 좌표 0에서 출구 좌표 L 까지 적분할 수 있으며 식(10)을 적분하면 식(11)과 같이 나타낼 수 있다.
여기서 ∆To는 Ts-Tm,o이고 ∆Ti는 Ts-Tm,i를 의미한다. 식(11)를 활용하여 총 대류열전달율을 계산하기 위해 식(5)를 식(12)와 같이 나타낼 수 있다.
또한 식(12)와 식(11)을 활용하면 식(13)과 같이 나타낼 수 있다.
식(13)에 식(5)를 다시 대입하면 평균 대류열전달 계수는 식(14)와 같이 나타낼 수 있다.
식(14)를 보면 평균 대류열전달 계수는 ṁ과 To에 의해 결정된다는 것을 알 수 있다. cp는 압력에 의존하지 않는 상수이며, P와 L은 일정 온도가 적용되는 치수를 의미하며 상수이다. 또한 일정 온도 조건이므로 Ts는 상수이고, 입구로 들어오는 유체의 온도 Ti 역시 상수이다. 즉 전산유체해석을 수행한 후 ṁ과 To를 추출함으로써 내부 유동에 대한 평균 대류열전달 계수를 구할 수 있다.
3. TPMS 구조의 대류열전달계수
3.1 단일격벽과 이중격벽 TPMS 모델링
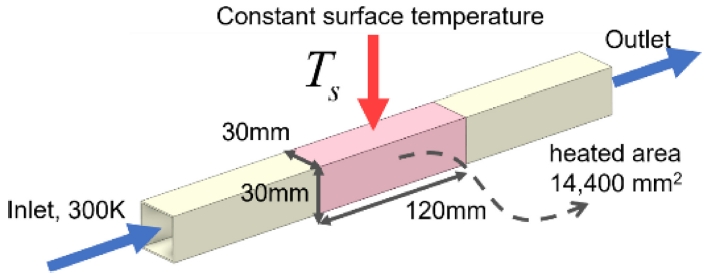
Fig. 2는 표면이 일정 온도로 유지되는 내부유동 해석모델이다. 30 × 120 mm 크기의 네 면에는 일정 온도 조건이 적용되며, 해석 영역 내부에는 단일격벽과 이중격벽 T P MS 구조가 적용되었다.
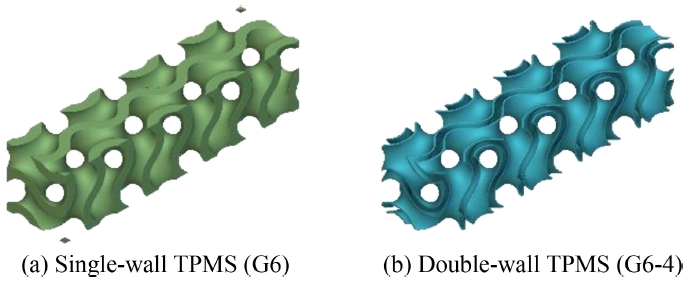
Fig. 3(a)는 두께가 6 mm인 단일격벽 Gyroid 구조(G6)이며,
Fig. 3(b)는 6mm 두께에서 4mm를 제거한 Gyroid 구조(G6-4)이다.
Table 1은 내부유동 해석에 적용된 TPMS 설계변수를 제시한다. TPMS 적용 영역의 크기는 30 × 30 × 120mm로, 단위셀 크기는 30 × 30 × 30mm이 1 × 4 배열로 구성하였다.
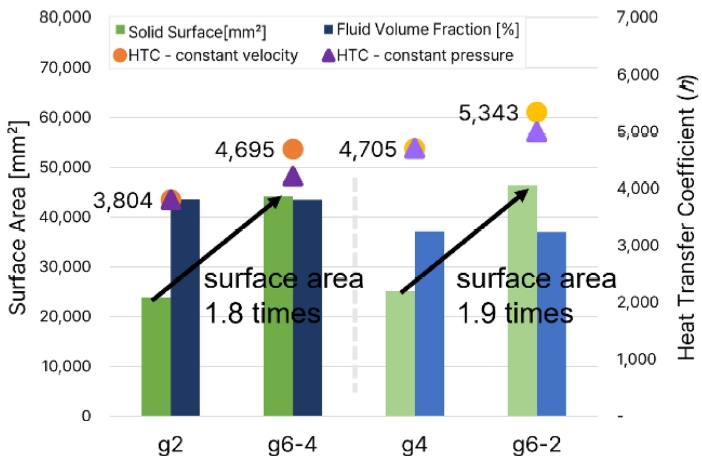
Table 2에서는 단일격벽과 이중격벽 T P MS 구조의 유체체적과 표면적을 비교하였다. G2 대비 G6-4는 동일한 유체체적 대비 표면적이 1.8배 증가하였고, G4 대비 G6-2는 1.9배 증가하였다. 표면적 확장에 따른 이중격벽의 열전달 성능을 확인하기 위해 G2와 G6-4, G4와 G6-2 구조를 비교 분석하였다.
Table 3은 내부유동의 해석조건이며 등속조건과 등압조건일때의 열전달성능을 함께 비교하였다.
계산 영역은 고체 구조와 유체 영역 모두 Ansys Fluent 2025 R1의 격자 생성 모듈을 통해 다면체 격자로 이산화하였다. 경계층은 10개 레이어로 구성하였으며, 최소 셀의 크기는 0.0003 m, 최대 셀의 크기는 0.003 m이다.
Table 4에 요약된 바와 같이, 각 구조의 고체 및 유체의 전체 셀 수는 약 35-62만개 수준이다. 모든 경우에서 직교성은 0.78 이상, Skewness는 0.22 이하로 해석에 적합한 품질을 확보하였다. 경계층 격자로 인해 Aspect Ratio가 다소 높게 나타났으나, 모든 값이 신뢰할 수 있는 해석 범위내에 있다.
Fig. 4는 G6-2 고체 및 유체 격자의 종단면을 보여준다.
표면적 확장으로 인한 대류열전달 성능 분석에 앞서 전산유체 해석의 신뢰성을 높이고자 에너지 보존 만족 여부를 확인하였다. 0.05 m/s의 속도로 유체가 흐를 때, 식(7)을 활용하여 평균 출구온도
Tm,o를 구하였으며, 식(8)을 통해 계의 평균 대류열전달률을 구하였다.
Table 5는 에너지 보존에 대한 결과이다. 각 해석모델의 에너지 오차가 26, 18, -89, 10 W 발생하였다. 식(15)에 의해 상대오차를 계산하였다.
Ėin은 입구 에너지 전달율,
Ėout은 출구 에너지 전달율,
Ėg은 생성되는 에너지율이다. 검사체적으로 유입된 총 에너지 대비 에너지 불균일성을 의미하며, 1% 내외의 수준임을 확인하였다. 이는 수치해석에 의한 오차로 에너지 보존 법칙이 성립한다는 것을 의미한다.
Table 6는 0.05 m/s로 일정하게 유입될 때의 CFD 해석 결과값을 나타냈다. 등속조건이므로 질량유량은 모두 일정하며, 출구영역에서의 평균온도는 이중격벽에서 더 높게 나타났다. 이에 따라 식(14)로 계산된 평균 대류열전달계수는 G2 대비 G6-4에서 1.2배, G4 대비 G6-2에서 1.1배 높았다. 다만, 압력 손실은 이중격벽에서 1.4배, 1.3배 증가하였다.
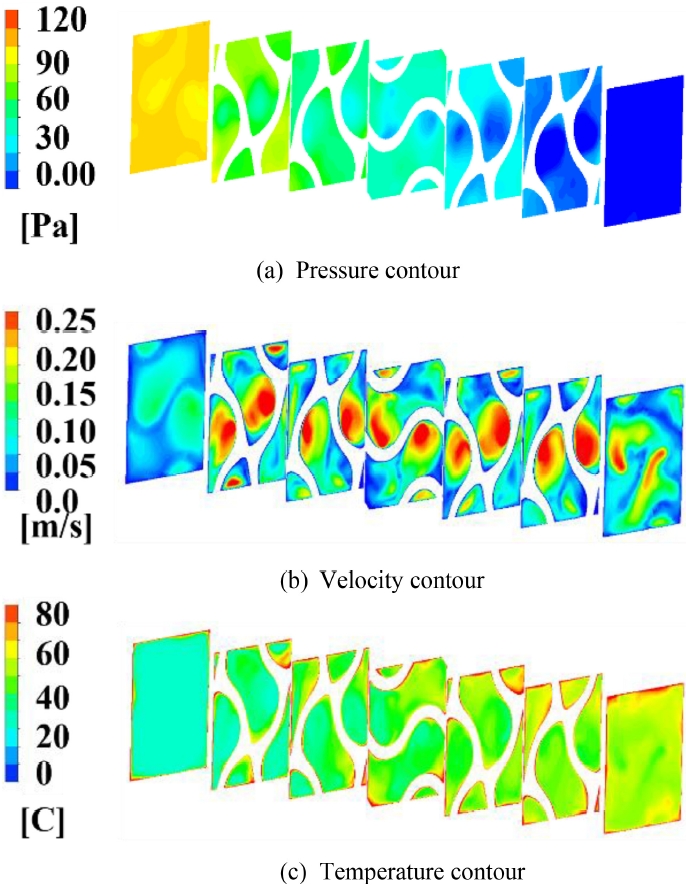
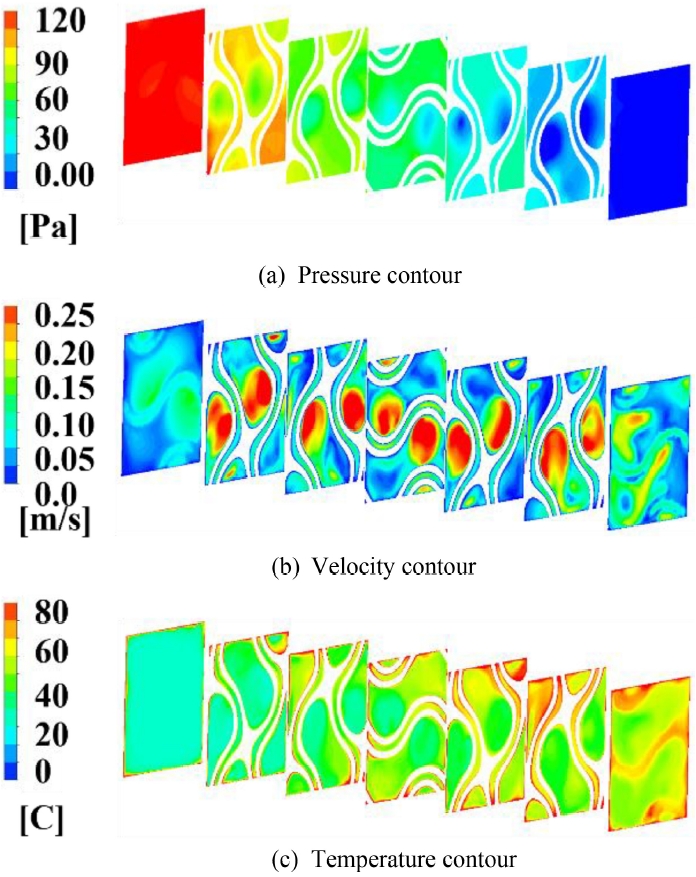
Fig. 5와
Fig. 6은 G4와 G6-4 구조에서 유체 흐름 방향을 따라 단면적의 압력, 속도, 온도 분포를 비교한 것이다. 동일한 유체 체적임에도 이중격벽에서 압력 손실이 증가한 것은 미세 유동 경로 형성으로 인해 속도 구배가 증가하고, 이에 따라 전단 응력이 커지기 때문이다. 전단 응력은 유동 방향과 반대되는 마찰력으로, 압력 손실은 전단 응력의 증가와 함께 증가한 것으로 해석된다.
단일격벽과 이중격벽의 압력 분포를 비교한 결과, 모든 유동 단면적 위치에서 압력이 낮은 영역이 관찰되었다(
Figs. 5(a)-
6(a)). 이 영역은 유체가 직선 경로로 관통하며 유동 저항이 최소화된 구간으로 판단된다.
Figs. 5(b) 및
6(b)의 속도 분포 결과, 유속 증가 영역이 낮은 압력 영역과 공간적으로 일치함을 확인하였다. 해당 영역의 온도 분포(
Figs. 5(c) 및
6(c))에서는 유체 온도가 상대적으로 낮았는데, 이는 유동의 저항이 감소하여 열전달 효율이 저하된 것으로 해석된다. 반면, 이중격벽 구조는 추가 생성된 유동 관로 주변의 유체 온도가 높은 것을 확인할 수 있다. 이는 이중격벽 구조의 표면적 확장으로 인해 대류 열전달 성능이 개선된 결과로 볼 수 있다.
등속조건에서 이중격벽의 출구 압력 손실이 단일격벽보다 큰 것을 확인하였다. 단일격벽과 동일한 압력 손실 조건에서도 대류열전달 성능이 향상되는지 확인하기 위해 등압 조건 해석을 수행하였다. G6-4의 압력 조건은 G2의 등속조건에서의 압력 손실 값과 동일하게 설정하였으며, G6-2는 G4의 압력 손실값을 기준으로 하였다.
Table 7은 등압조건 CFD 해석 결과를 요약하였다.
이중격벽은 등속조건 대비 낮은 압력 환경에서 작동하므로, 질량 유량이 단일격벽보다 낮아지는 것을 확인하였다. 질량 유량 감소로 열 교환량이 감소할 수 있음에도 불구하고 일중격벽에서 출구 온도의 평균이 높게 유지되었으며, 이는 표면적 확장에 따른 열전달 효율 증가로 해석된다. 식(14)로 계산한 평균 대류열전달계수는 압력 조건 하강 및 질량 유량 감소에도 불구하고, 이중격벽에서 각각 1.1배, 1.06배 증가하였다. 따라서, 동일한 유체 체적 내에서 표면적 확장을 통해 대류 열전달 성능을 향상시킬 수 있음을 확인하였다.
Fig. 7은 단일격벽과 이중격벽 T P MS 구조의 평균 대류열전달계수를 표면적 확장에 따라 비교한 그래프이다. G2와 G6-4의 유체체적은 유사한 체적을 가지고 있으며 G6-4에서 표면적이 1.8배 증가함에 따라 등속조건(●)과 등압조건(▲) 모두에서 이중격벽 구조의 열전달 성능이 향상됨을 보여준다. 마찬가지로 G4와 G6-2의 유체체적은 동일한 수준을 보이며, G6-2에서 표면적이 1.9배 증가하였을 때, 등속조건과 등압조건에서의 평균 대류열전달계수가 증가하는 것을 나타냈다.
4. 결론
본 연구는 T P MS가 적용된 내부유동에서의 열전달 성능을 비교하기 위해 먼저 에너지 보존을 만족하는 것을 확인하였으며 단일격벽(G2, G4)과 이중격벽 TPMS (G6-4, G6-2)의 표면적 확장에 따른 열전달 성능을 분석하였다.
전산유체해석에서 에너지 평형을 만족시키기 위해 입열 에너지와 대류 열전달로 인한 출입구 및 배출구에서의 열전달률 값 산출이 중요하다. 입구와 출구의 단면적에 대한 온도, 속도, 단면적 평균온도의 계산을 통해 에너지 균형을 확인한 결과, 1% 내외의 상대오차를 보였다. 이는 수치 해석 모델의 에너지 보존을 입증한다.
G2와 G6-4의 경우 동일한 유체체적을 보유하지만 G6-4의 표면적이 1.8배 넓은 것을 확인하였으며, G4와 G6-2 역시 동일한 유체체적임에도 G6-2의 표면적이 1.9배 크다는 것을 확인하였다. 이를 통해 이중격벽 구조가 단일격벽과 동일한 유체체적임에도 표면적을 효과적으로 확장시킬 수 있음을 증명하였다.
등속조건의 내부유동에서 G6-4는 G2에 비해 출구영역의 평균온도가 높았으며 G6-2 또한 G4에 비해 출구영역의 평균온도가 높음을 전산유체해석을 통해 확인하였다. 확장된 표면적으로 인해 유체로의 열전달이 증가하였음을 온도 분포의 유동 단면적을 통해 확인하였다.
이중격벽 T P MS의 열전달성능을 정량적으로 평가하기 위해 평균 대류열전달계수를 계산하였다. 등속조건에서의 질량유량은 모든 구조에서 동일하므로, 평균 대류열전달계수 산출에 사용된 값은 출구의 평균온도이다. G6-4와 G6-2의 평균 대류열전달계수는 G2와 G4에 비해 1.4배, 1.3배 증가하였다. 다만, 동일한 유체체적이지만 G6-4와 G6-2에서의 압력손실이 높은 이유는 미세 관로 형성으로 인한 전단응력 증가 때문으로 판단된다.
이중격벽의 압력손실이 더 크다는 것은 단일격벽과 이중격벽의 유동이 등압조건으로 주어졌을 때, 이중격벽의 질량유량이 감소함을 의미한다. 이에 따라 등압조건에서 해석을 수행하였고, 이중격벽에서도 열전달성능을 정량적으로 평가하였다. 등압조건의 평균 대류열전달계수 산출에는 질량유량과 출구 온도 평균값이 사용된다. 결과적으로 등압조건의 G6-4와 G6-2의 평균 대류열전달계수는 G2, G4 대비 각각 1.1배, 1.06배 증가함을 확인하였다.
이러한 결과는 이중격벽 TPMS 구조가 유체와의 접촉면을 증가시켜 열전달 효율을 향상시켰다. 반면 복잡한 유로 형성은 전단응력과 압력손실을 증가시키므로 냉각 성능과 유동 저항 간의 trade-off를 고려한 최적 설계가 요구된다. 특히 등압 조건에서는 질량유량 감소가 전체 열전달 성능 증가를 제한하는 요인이 되며, 이는 실제 시스템에 적용시 성능 향상을 결정짓는 요소가 될 수 있다. 본 연구 결과를 통해 제한된 공간 내에서 높은 열전달 성능이 요구되는 전자 장비, 반도체 장비 냉각 등 냉각 시스템에 효과적으로 적용될 수 있다. 또한, 적층제조를 통해 구현한다면 기존 냉각시스템 보다 우수한 열전달 성능을 기대할 수 있다.
FOOTNOTES
-
ACKNOWLEDGEMENT
본 논문은 2025년도 정부(방위사업청)의 재원으로 국방기술진흥연구소의 지원을 받아 수행된 연구이며, 이에 감사드립니다 (No. KRIT-CT-23-042, 터보팬 내열부품용 3D프린팅 내열합금 개발 기술).
Fig. 1Control volume for internal flow
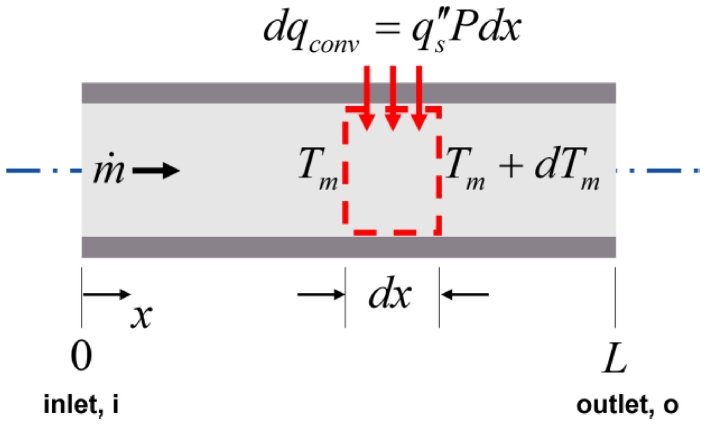
Fig. 2Topology for analysis model

Fig. 3Structures of single- and double-wall gyroid TPMS
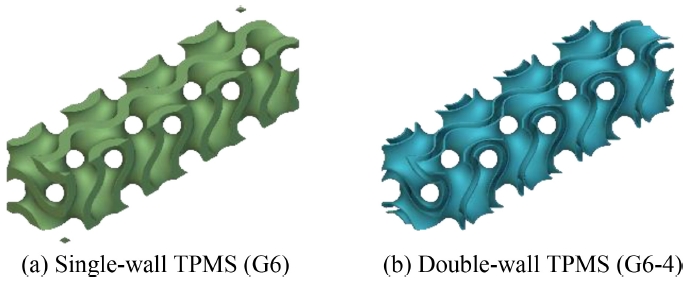
Fig. 4Side view of G6-2 solid and fluid region mesh

Fig. 5G4 contour under constant velocity
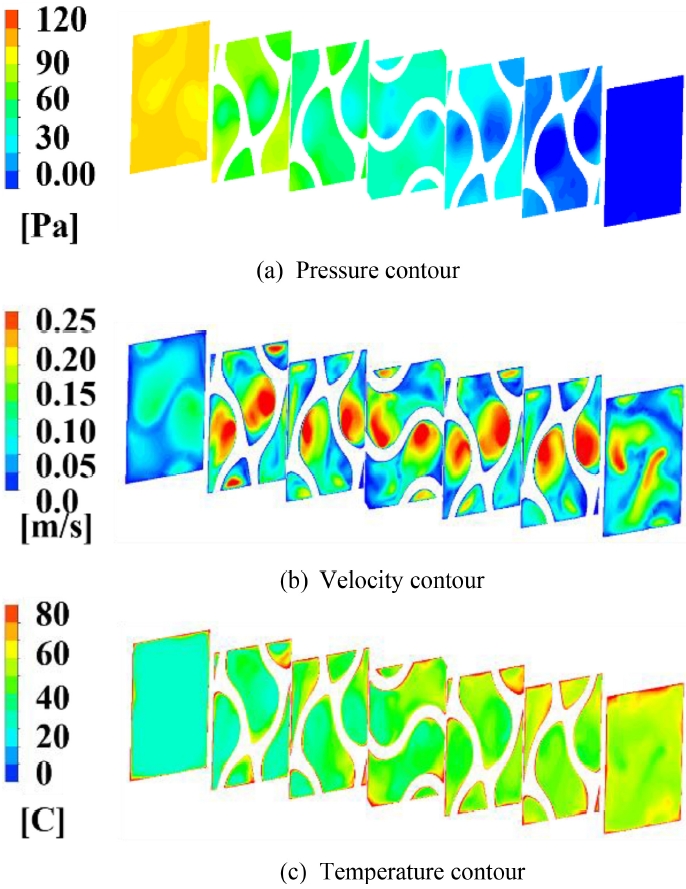
Fig. 6G6-2 contour under constant velocity
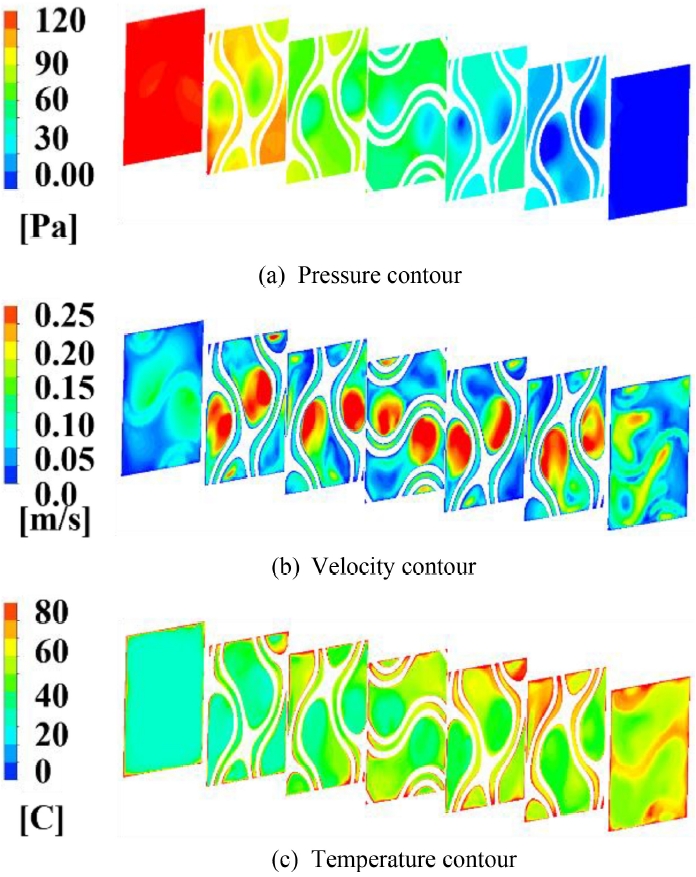
Fig. 7Comparison of convective heat transfer coefficient of doublewall and single-wall TPMS according to surface area expansion
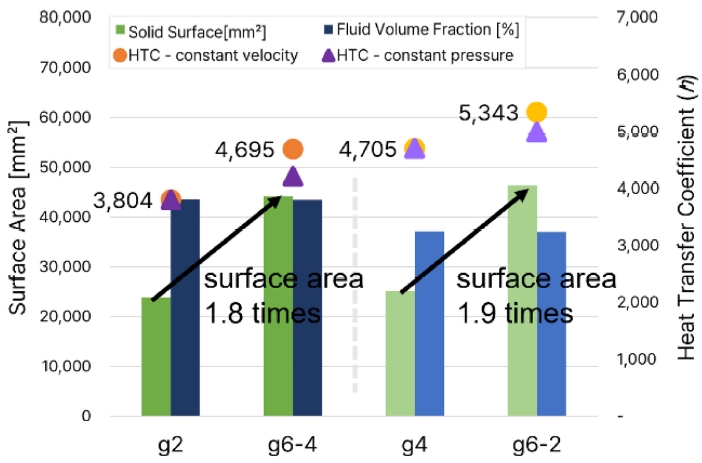
Table 1
Table 1
|
Size of design space [mm3] |
30 × 30 × 120 |
|
Unit cell size [mm3] |
30 × 30 × 30 |
|
Single-wall sheet-based TPMS |
G2, G4 |
|
Double-wall sheet-based TPMS |
G6-4, G6-2 |
Table 2Geometrical characteristic of single-wall and double-wall
Table 2
|
Surface [mm] |
Fluid volume [mm3] |
|
G2 |
6,102 |
23,521 |
|
G6-4 |
11,212 |
23,465 |
|
G4 |
6,569 |
20,025 |
|
G6-2 |
11,932 |
19,968 |
Table 3
Table 3
|
Turbulence model |
SST k-ω
|
|
Fluid specific heat [J/(kg∙K)] |
4,182 |
|
Heating temperature [K] |
373.15 |
|
Inlet temperature [K] |
300.00 |
|
Outlet pressure [Pa] |
0 |
Table 4Mesh quality and cell statistics for each case
Table 4
|
Total cell number |
Orthogonal quality |
Skewness |
Aspect ratio |
|
G2 |
348,167 |
0.835 |
0.165 |
11.66 |
|
G6-4 |
491,154 |
0.786 |
0.214 |
14.08 |
|
G4 |
373,335 |
0.831 |
0.169 |
8.88 |
|
G6-4 |
625,162 |
0.814 |
0.186 |
11.57 |
Table 5Energy conservation of analysis model
Table 5
|
Total heat transfer rate [W]
|
Energy error [W] |
Relative error [%] |
|
Heat |
Inlet |
Outlet |
|
G2 |
3,688 |
347 |
4,009 |
26 |
0.59 |
|
G6-4 |
4,379 |
347 |
4,708 |
18 |
0.35 |
|
G4 |
4,366 |
347 |
4,802 |
-89 |
1.72 |
|
G6-2 |
4,854 |
347 |
5,191 |
10 |
0.18 |
Table 6Results for constant velocity conditions
Table 6
|
G2 |
G6-4 |
G4 |
G6-2 |
|
Mass flow [kg/s] |
0.05 |
0.05 |
0.05 |
0.05 |
|
Pressure [Pa] |
54.1 |
76.7 |
96.8 |
123.0 |
|
Outlet temperature [K] |
319.6 |
323.3 |
323.4 |
325.9 |
|
h̅L [W/(m2·K)] |
3,804 |
4,695 |
4,705 |
5,343 |
Table 7Results for constant pressure conditions
Table 7
|
G2 |
G6-4 |
G4 |
G6-2 |
|
Mass flow [kg/s] |
0.05 |
0.036 |
0.05 |
0.038 |
|
Pressure [Pa] |
54.1 |
54.1 |
96.8 |
96.8 |
|
Outlet temperature [K] |
319.6 |
325.3 |
323.4 |
327.9 |
|
h̅L [W/(m2·K)] |
3,804 |
4,215 |
4,705 |
4,992 |
REFERENCES
- 1. Nagesha, B., Dhinakaran, V., Shree, M. V., Kumar, K. M., Chalawadi, D., and Sathish, T., (2020), Review on characterization and impacts of the lattice structure in additive manufacturing, Materials Today: Proceedings, 21, 916-919.
- 2. Yue, X., Shang, J., Zhang, M., Hur, B., and Ma, X., (2022), Additive manufacturing of high porosity magnesium scaffolds with lattice structure and random structure, Materials Science and Engineering: A, 859, 144167.
- 3. Sarabia-Vallejos, M. A., Rodríguez-Umanzor, F. E., González-Henríquez, C. M., and Rodríguez-Hernández, J., (2022), Innovation in additive manufacturing using polymers: A survey on the technological and material developments, Polymers, 14(7), 1351.
- 4. Feng, J., Fu, J., Yao, X., and He, Y., (2022), Triply periodic minimal surface (TPMS) porous structures: From multi-scale design, precise additive manufacturing to multidisciplinary applications, International Journal of Extreme Manufacturing, 4(2), 022001.
- 5. Yeranee, K., and Rao, Y., (2022), A review of recent investigations on flow and heat transfer enhancement in cooling channels embedded with triply periodic minimal surfaces (TPMS), Energies, 15(23), 8994.
- 6. Khan, N., Acanfora, V., and Riccio, A., (2024), Non-conventional wing structure design with lattice infilled through design for additive manufacturing, Materials, 17(7), 1470.
- 7. Kim, J., and Yoo, D., (2020), A design and fabrication method of new compact heat exchangers using triply periodic minimal surface, Journal of the Korean Society for Precision Engineering, 37(7), 509-518.
- 8. Park, S., Lee, J., Lee, S., Sung, J., Jung, H., Lee, H., and Kim, K., (2025), Temperature uniformity control of 12-inch semiconductor wafer chuck using double-wall TPMS in additive manufacturing, Materials, 18(1), 211.
- 9. Kim, K., Park, S., Lee, S., Gu, S., Jung, H., and Lee, J., (2024), Optimal design of gyroid solid-TPMS structures for 8-inch wafer prober lower chuck in additive manufacturing, Journal of Mechanical Science and Technology, 38(9), 4563-4570.
- 10. Incropera, F. P., DeWitt, D. P., Bergman, T. L., Lavine, A. S., (2017), Incropera's principles of heat and mass transfer, Global Edition, 8th Edition, Wiley.
Biography
- Sohyun Park
M.S. candidatate in the Department of Robot and Smart System Engineering, Kungpook National University. Her research interest is design for additive manufacturing.
- Jihyun Sung
Ph.D., Principal Researcher Director in Daegyeong Tech. Application Division, KITECH. His research interest is additive manufacturing.
- Dahye Kim
Principal Researcher at Korea Institute of Industrial Technology. Her research interest is Additive Manufacturing.
- Kunwoo Kim
Ph.D. candidate in the Daegyeong Technology Application Division, Korea Institute of Industrial Technology. His research interest is metal and plastic based design for additive manufacturing.