ABSTRACT
Coherent Beam Combining (CBC) is a promising technique for enhancing laser output power by accurately aligning the phase and position of multiple laser beams. The Stochastic Parallel Gradient Descent (SPGD) algorithm is commonly used in CBC systems due to its simplicity and scalability. However, its dependence on fixed control parameters can result in slow convergence rates and diminished control stability. To overcome these challenges, this study introduces an adaptive SPGD algorithm that dynamically adjusts the perturbation amplitude and learning rate based on the real-time value of the objective function. This approach accelerates convergence during the initial stages by increasing control inputs when the objective function value is low, while ensuring stability as the function nears its maximum in later stages. Numerical simulations of 7-channel and 19-channel CBC systems revealed that the adaptive SPGD algorithm reduced average iteration counts by 26.4% and 18.1%, respectively, compared to the basic SPGD. Furthermore, the overall control performance improved, achieving high beam combining efficiency with reduced total computation time. This proposed algorithm serves as a straightforward yet effective enhancement to the conventional SPGD method, improving both convergence speed and stability.
-
KEYWORDS: Coherent beam combining, Stochastic parallel gradient descent, Adaptive control, Phase control, Tip-tilt control
-
KEYWORDS: 결맞음 빔결합, SPGD, 적응형 제어, 위상 제어, 팁-틸트 제어
NOMENCLATURE
Objective Function at the nth Iteration
Control Input of the ith Channel
Adaptive Gain Coefficient at the nth Iteration
Learning Rate at the nth Iteration
Minimum Perturbation Amplitude
Electric Field at the Target Plane
Distance from the Beam Center
Amplitude of Electric Field
Beam Intensity at Target Plane
1. 서론
레이저 용접, 레이저 무기 시스템과 같은 다양한 응용 분야에서 레이저의 최대 출력은 시스템의 핵심 요구 성능 중 하나로 간주된다[
1,
2]. 그러나 단일 채널 레이저가 생성할 수 있는 출력에는 광학 부품의 허용 손상 한계와 출력 증가에 따른 발열 문제로 인해 물리적 제한이 존재한다. 이러한 한계를 극복하기 위해 다채널 레이저를 목표 위치에서 결합하여 최종 출력을 증가시키는 결맞음 빔결합(Coherent Beam Combining, CBC) 기술이 제안되었다[
3-
5].
결맞음 빔결합은 각 채널이 동일한 파장의 빔을 방출하고, 목표 위치에서 모든 빔이 동일한 위상을 가지며 결합하도록 위상 및 위치를 정밀하게 제어하는 방식이다. 각 채널별로 지속적인 위상 제어가 필요해 시스템의 복잡성이 높아지지만, 간섭 효과를 통해 결합된 빔의 최대 세기가 채널 개수의 제곱에 비례하여 증가한다는 장점을 가진다. 이러한 특성 덕분에 결맞음 빔결합은 출력 확장성이 뛰어나며, 고출력 레이저가 요구되는 국방 및 산업 분야에서 활발히 연구되고 있다[
6,
7].
결맞음 빔결합 시스템은 각 채널의 위상을 제어하는 위상 변조기(Phase Modulator)와, 파면 보정 및 위치 제어를 수행하는 팁-틸트 액추에이터(Tip-tilt Actuator)로 구성된다. 이때, 위상과 팁-틸트를 동시에 제어하기 위한 방법 중 하나로 확률적 병렬 경사 하강법(Stochastic Parallel Gradient Descent, SPGD)이 사용된다. SPGD는 입력값에 임의의 섭동을 추가한 후, 이에 따른 빔 세기 변화를 측정하여 빔 세기를 증가시키는 방향으로 입력을 조정하는 피드백 방식의 알고리즘이다. 즉, 목표 지점에서의 빔 세기 정보만을 활용하므로 시스템 구성이 비교적 단순하며, 연산 또한 간단해 채널 개수가 증가하더라도 타 알고리즘에 비해 계산 비용이 크게 증가하지 않는다는 장점을 가진다.
그러나 SPGD 방법은 고정된 파라미터를 사용하기 때문에 제어 안정성과 수렴 속도 사이의 상충 관계를 가지고 있어, 달성할 수 있는 제어 성능에 한계가 있다. 이를 극복하기 위해 다양한 적응형 SPGD 알고리즘들이 제안되었다. Hu와 Che 등은 Adam 최적화 방법을 응용하여 누적 기울기에 따라 학습률을 동적으로 조정하는 적응형 알고리즘을 제시하였으며, 이를 통해 기존 SPGD보다 빠른 수렴 속도를 보였다[
8,
9]. Vorontsov와 Weyrauch 등은 목표 지점의 빔 세기를 이론적 최댓값과 비교하고, 이를 기반으로 학습률과 섭동 크기를 조정하는 적응형 기법을 제안하여, 기존 SPGD 알고리즘 대비 높은 빔 세기와 빠른 수렴 속도를 달성하였다[
10-
12]. 그러나 기존 적응형 SPGD 알고리즘들은 SPGD의 기본 파라미터인 섭동 크기 및 학습률 뿐만 아니라 이를 실시간으로 조정하기 위한 추가 파라미터를 필요로 한다. 이때, 섭동 크기와 학습률, 그리고 적응형 파라미터가 서로 영향을 미치기 때문에 독립적인 최적화가 어려우며, 최적의 파라미터를 찾는 데 많은 시간이 소요되는 문제가 있다.
이에 본 논문에서는 독립적인 파라미터 최적화를 통해 적절한 파라미터를 신속하게 도출할 수 있으면서도, 위상 및 팁-틸트 제어 안정성과 높은 수렴 속도를 동시에 달성할 수 있는 새로운 적응형 SPGD 알고리즘을 제안하고 그 특성을 분석하였다. 또한, 제안하는 알고리즘의 성능을 검증하기 위해 제어 시뮬레이터를 구축하였고, 기존 SPGD 기법과의 비교 분석을 통해 효용성을 평가하였다.
2. 적응형 SPGD 알고리즘 작동원리
2.1 기존 SPGD 알고리즘
결맞음 빔결합 시스템은
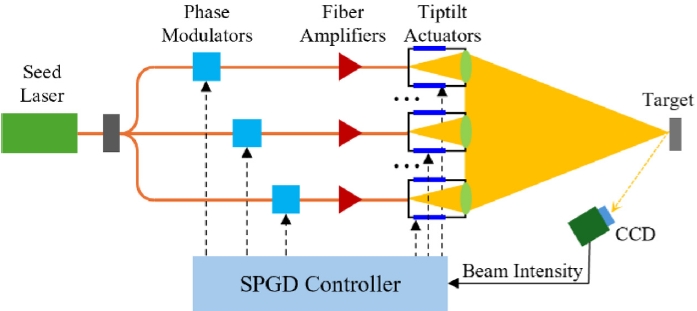
Fig. 1에 나타낸 바와 같이 목표 지점으로 각 채널의 빔을 집중시키고 위상을 일치시키기 위해, 모든 채널의 위상 변조기와 팁-틸트 액추에이터의 입력을 제어한다. 이때 각각의 레이저 빔이 대기를 통과해 만들어지는 위상과 파면의 정확한 모델링이 어려워 주로 모델-프리 최적화(Modelfree Optimization) 기반의 제어 방법이 활용되며, 그중 대표적인 방법이 SPGD 방법이다. SPGD는 임의의 섭동을 양의 방향과 음의 방향으로 인가한 후, 목적함수 값의 변화를 비교하여 기울기(Gradient)를 근사적으로 추정하는 방식으로 동작한다. 이 기울기 정보를 이용하여 입력값을 점진적으로 업데이트함으로써 최종 빔 세기가 증가하는 방향으로, 즉 각 채널의 위상과 위치를 한 곳으로 집중하는 제어가 이루어진다.
SPGD 방법을 위한 목적함수 J = J(u1, …,uN)는 목표 지점의 빔 세기를 이론적인 최댓값으로 표준화한 값을 사용한다. N개의 채널 입력 {ui}(i=1,…,N)에 평균이 0, 분산이 σ2인 정규분포를 따르는 임의의 작은 섭동 {δui}을 각각 인가하면, 이에 따른 목적함수는 식(1)과 식(2)와 같이 나타낼 수 있다.
이때, 목적함수의 변화량 δJ = J+-J-를 Taylor 급수로 전개하면 식(3)으로 표현된다.
식(3)에 δul를 곱하면 식(4)와 같이 정리할 수 있다.
여기서 Hl는 고차항의 합으로, 식(5)와 같이 정의된다.
이때, 각 섭동
δui가 통계적으로 독립적인 변수이므로,
Hl의 기댓값은 0이 된다[
13]. 따라서,
δJδul의 평균값은 (
∂J/∂ul)에 비례하며, 이를 통해 기울기가 근사적으로 구해진다.
이렇게 추정한 기울기를 바탕으로 SPGD는 각 채널 입력을 다음과 같은 규칙에 따라 업데이트함으로써 평균적으로 J를 증가시킬 수 있다.
이때 α는 기울기 방향으로의 입력 변화량을 조절하기 위해 사용하는 상수로 학습률이라 부르며, 목적함수 J의 증가를 위해 양의 값을 사용한다.
2.2 적응형 SPGD 알고리즘
기존 SPGD 알고리즘에서는 섭동 분포의 크기나 학습률의 설정이 제어 성능 및 수렴 속도에 큰 영향을 미친다. 먼저, 섭동 크기나 학습률이 지나치게 크면, 목적함수가 수렴하지 못하고 큰 변동을 일으켜 결맞음 빔결합 시스템의 안정성을 저하시킬 수 있다. 특히, 알고리즘 초기에는 적절하게 설정된 파라미터라도, 빔이 수렴하고 위상이 대부분 일치하게 되면 목적함수 값의 변동폭이 증가하여 진동이 발생할 수 있다. 반대로, 섭동 크기나 학습률이 너무 작은 경우, 수렴 속도가 현저히 저하되어 실시간 위상 보상 및 위치 제어의 요구 조건을 충족하지 못할 가능성이 높다. 이처럼 SPGD 알고리즘은 파라미터 설정에 따라 수렴 속도와 제어 안정성 사이의 상충관계를 가지게 된다.
이에 따라, 본 논문에서는 섭동 크기와 학습률을 목적함수 값에 따라 능동적으로 조절함으로써, 빠른 수렴과 제어 안정성을 동시에 달성하는 적응형 SPGD 알고리즘을 제안하였다. 적응형 SPGD 알고리즘에서는 섭동 크기와 학습률을 지수 함수를 활용해 다음과 같이 조절한다.
여기서 γ는 파라미터 크기를 조절하는 이득 상수로 1보다 큰 값을 사용하며, σmin과 αmin은 각각 섭동 크기와 학습률의 최솟값을 나타낸다. 위 식에 따라, 알고리즘 초기에는 목적함수값이 작아 γ(1-J(n))값이 상대적으로 크기 때문에 섭동 크기와 학습률이 크게 설정된다. 반면, 목적함수 값이 이론적 최댓값인 1에 근접하면 γ(1-J(n))값이 작아져 섭동 크기와 학습률이 최솟값에 수렴한다.
따라서, 각 파라미터의 최솟값 σmin, αmin을 기본 SPGD에서 안정적인 수렴 성능을 보이는 값으로 설정하면, 적응형 SPGD의 수렴 안정성을 확보할 수 있다. 또한, 섭동 크기와 학습률이 작아 수렴 속도가 저하되는 문제는, 파라미터 이득 상수 γ를 조절하여 초깃값을 증가시킴으로써 극복할 수 있다. 조절된 파라미터를 이용한 적응형 SPGD 알고리즘의 입력 업데이트 규칙은 식(9)와 같다.
여기서, 각 파라미터
σmin,
αmin,
γ의 값은 위상 제어와 팁-틸트 제어를 위해 개별적으로 최적화될 필요가 있다. 이때
σmin,
αmin는 기존 SPGD 알고리즘에서 사용된 섭동 크기 및 학습률을 그대로 적용할 수 있으므로, 추가적인 조정 없이 이득 상수
γ만 최적화하면 된다. 따라서, 제안된 방법은 기존 연구에서 제시된 알고리즘에 비해 파라미터 최적화 과정이 단순하며, 동시에 빠른 수렴 속도와 높은 안정성을 제공할 수 있다. 기존 SPGD 알고리즘과 제안된 적응형 SPGD 알고리즘의 작동 원리를
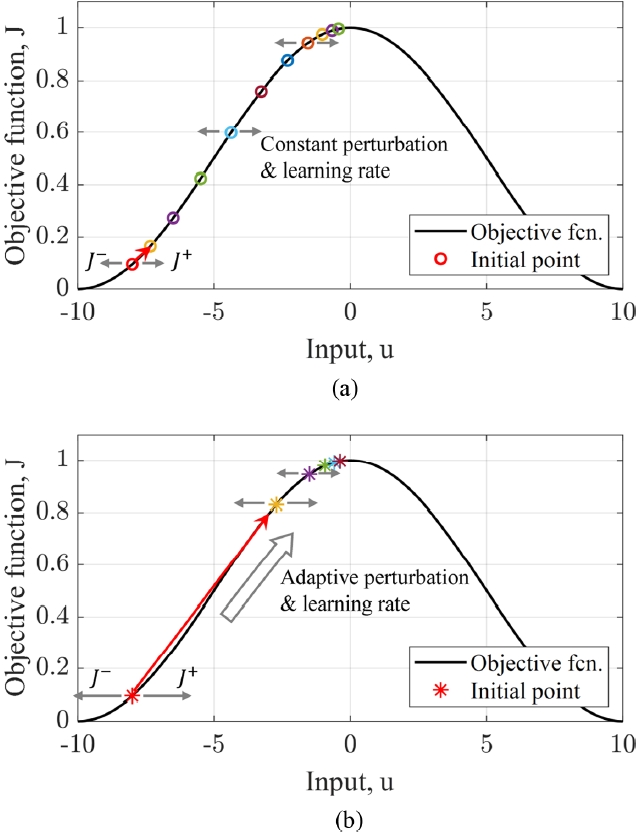
Fig. 2에 나타내었다. SPGD 알고리즘은 섭동 크기와 학습률이 일정해 느린 수렴 속도를 보이는 반면, 적응형 SPGD 알고리즘은 초반의 큰 파라미터로 인해 빠른 속도로 수렴하는 것을 확인할 수 있다.
3. 빔 모델링과 위상 및 팁-틸트 능동제어 시뮬레이터
3.1 빔 모델링
본 연구에서는 결맞음 빔결합 상황을 모사하기 위해 타겟 평면에서 다채널 빔의 위상 차이에 따른 상쇄 보강 간섭 관계를 활용하였다. 먼저 단일 빔의 경우 타겟 평면에서 시간에 따라 진동하는 광학 전기장으로 나타낼 수 있으며, 이는 식(10)과 같이 표현된다.
여기서 ω0은 시간 t에 따른 진동 주파수, ρ는 빔의 중심 r0로부터의 반경 방향 위치 벡터로, ρ=r-r0로 정의된다. M(ρ)은 위치 ρ에 따른 rectangular 함수로, 빔 내부 영역에서는 1, 외부 영역에서는 0의 값을 갖는다. 전기장의 세기 A(ρ)는 빔 중심으로부터 반경방향 거리 |ρ|에 따라 식(11)과 같이 가우시안 분포로 정의된다.
여기서 A0는 최대 전기장 세기, a0는 가우시안 분포의 반경을 나타내며, φ0은 빔 중심 위치 변화에 따른 위상 오프셋을 나타낸다. 타겟 평면에서의 단일 빔의 세기 분포는 전기장의 크기의 제곱으로 나타나므로, I(ρ,t)=|E(ρ,t)|2와 같이 표현되며, 빔 내부 영역에서는 식(12)로 나타난다.
이때 빔의 최대 세기는 I0=A02이다.
3.2 위상 및 팁-틸트 시뮬레이터
결맞음 빔결합을 구현하기 위해서는 개별 빔의 위상을 정밀하게 제어하고, 팁-틸트 제어를 통해 빔의 방향과 위치를 조정해야 한다. 먼저 위상을 제어하는 경우, 식(10)에 추가적인 위상 제어 항 φc을 포함하여 빔의 광학 전기장을 식(13)으로 표현할 수 있다.
팁-틸트 제어는 타겟 평면에서 빔 중심의 위치 r0를 변화시키며, 이때 빔의 위상 오프셋 φ0도 함께 변화한다.
다수 빔이 존재하는 경우 타겟 평면에서의 총 전기장은 각 빔의 광학 전기장이 절대 좌표 r에서 중첩된 결과로 식(14)으로 표현된다.
여기서 N은 빔 채널 수를 의미하며, 채널별로 위상 오프셋 φ0, i과 제어된 위상 φc, i 값이 결정된다. 마찬가지로 총 빔 세기 분포는 식(15)와 같이 계산된다.
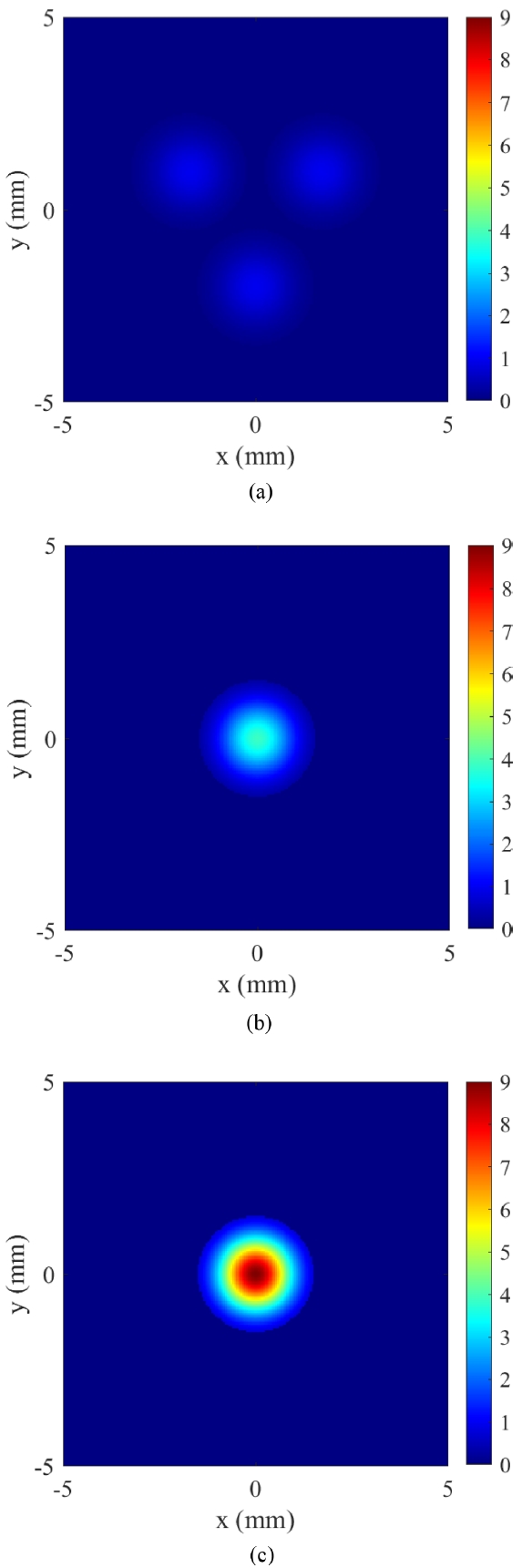
Fig. 3는 가로, 세로 각각 10mm인 타겟 평면에서 다수 빔의 중첩 과정을 시각적으로 보여준다.
Fig. 3(a)는 조리개 직경이 3 mm이고, 반경
a0 = 0.45 mm인 가우시안 분포를 가지는 중첩되지 않은 3개 채널의 빔을 보인다. 각각의 빔은 최대 세기 1을 가지는 것으로 표준화되었으며 전혀 중첩되지 않은 상태로 서로 다른 중심 위치를 가질 때의 모습을 보여준다.
Fig. 3(b)는 각 빔이 타겟 평면의 (0,0) 부근으로 중첩되었으나, 서로 다른 위상을 가지는 상태를 나타낸다. 이 경우 최대 빔 세기는 단일 빔과 비교하였을 때에 증가하지만, 위상이 서로 맞지 않아 완벽한 중첩이 이루어지지는 않는다.
Fig. 3(c)는 모든 빔이 동일한 위치 (0,0)에서 동일한 위상을 가지며 중첩된 상태를 보여준다. 이 경우 같은 지점에서 완전한 위상 잠금이 이루어져 중심에서의 빔 세기가 최댓값에 도달하며, 이론적으로 완벽한 중첩이 이루어졌음을 확인할 수 있다.
Fig. 3(b)에서 나타난 바와 같이 팁-틸트 제어를 통해 타겟 평면에서의 빔 위치가 동일하다고 하더라도 위상이 동일하지 않은 경우 이론적인 최댓값에 미치지 못함을 확인할 수 있다. 따라서 결맞음 빔결합의 최대 효율을 달성하기 위해서는 타겟 평면에서 모든 빔의 중심 위치가 일치해야 하며, 각 빔의 위상도 정렬되어야 한다. 본 연구는 이러한 조건을 만족시키기 위한 알고리즘을 고안하였고, 기존 SPGD 알고리즘 대비 개선된 성능을 비교 분석하고자 한다.
3.3 위상 및 팁-틸트 제어 알고리즘 성능평가
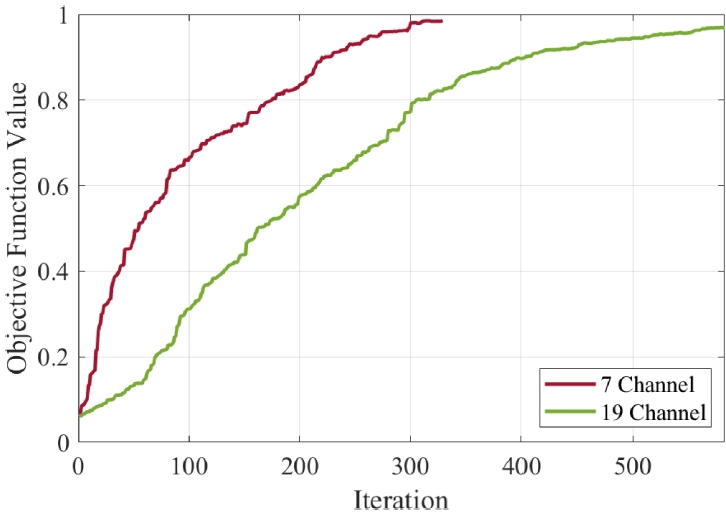
Fig. 4는 앞서 설명한 시뮬레이터 환경에서 기존 SPGD 알고리즘의 동작 예시를 나타낸다. 목적함수 값은 모든 채널의 빔 위상이 정렬되어 완벽한 결맞음 상태를 이루고, 팁-틸트 제어를 통해 타겟 평면에서 동일한 지점에 정렬된 이상적인 결합 상태를 기준으로 정규화 되었다. 따라서 목적함수 값이 1에 가까울수록 빔이 효과적으로 결합되었음을 의미한다. 본 연구에서는 단일 시행에서의 알고리즘 성능 평가를 위해 목적함수 수렴까지의 반복 횟수 및 최종 수렴 값을 주요 지표로 활용하였다. 예를 들어,
Fig. 4에서 7채널 빔결합의 경우 328회의 반복 후 최종 목적 함수 값이 0.985에 도달하였으며, 19채널의 경우 583회의 반복 후 0.969에 도달하였다.
알고리즘의 종료 조건은 목적함수 값의 변화 추이를 기반으로 설정되었다. 최근 20개의 목적함수 값의 표준편차가 이론적 최댓값의 0.1% 수준으로 작아질 경우 목적함수가 수렴한 것으로 판단하여 알고리즘을 종료하였다. 다른 경우로, 가장 최근의 목적함수 값이 50회 반복 이전의 목적함수 값보다 작은 경우, 알고리즘이 수렴하지 못하고 발산하거나 진동하는 것으로 간주하여 종료하였다.
기존 SPGD 알고리즘의 경우, 섭동 크기와 학습률과 같은 파라미터가 알고리즘의 수렴 특성과 성능에 큰 영향을 미친다. 본 연구에서는 파라미터 범위 탐색(Sweep)을 수행하여, 독립 시행 중 70% 이상이 0.90 이상의 목적함수 값을 달성하는 파라미터 영역을 선별하고, 그 중 평균 수렴 시간이 최소가 되는 파라미터를 최종적으로 채택하였다.
모든 시뮬레이션은 각 채널의 빔이 임의의 초기 위상을 가지며, 초기 위치가 빔 반경 내에서 임의의 편차를 갖는 조건에서 수행되었다. 알고리즘의 성능 평가는 각 조건에 대해 10,000회의 독립 시뮬레이션을 수행한 후, 그 평균 결과를 통해 분석하였다. 추가로, 본 연구는 다양한 초기 조건에서의 알고리즘 성능 비교 및 수렴 특성 분석에 초점을 맞추었기 때문에, 반복 과정에서 발생할 수 있는 외부 대기 환경의 변동이나 제어 노이즈는 포함하지 않았다.
4. 적응형 SPGD 알고리즘 시뮬레이션 결과 및 제어 성능 분석
앞서 2장에서 서술한 바와 같이, 본 연구에서 제안하는 적응형 SPGD 알고리즘은 목적함수 값이 낮은 초기 단계에서는 기존 SPGD 알고리즘에서 설정된 파라미터 값을 증가시켜 제어 입력의 변화를 상대적으로 크게 유도함으로써 목적함수 값이 빠르게 증가하도록 설계되었다. 이후 목적함수 값이 증가하여 1에 가까워지는 과정에서는 파라미터 크기를 점진적으로 감소시켜 기존에 설정된 파라미터 값과 유사한 수준으로 수렴하도록하여, 알고리즘의 안정성을 확보하였다. 적응형 파라미터 값의 변화 정도는 파라미터 이득 상수 γ를 통해 조정될 수 있다.
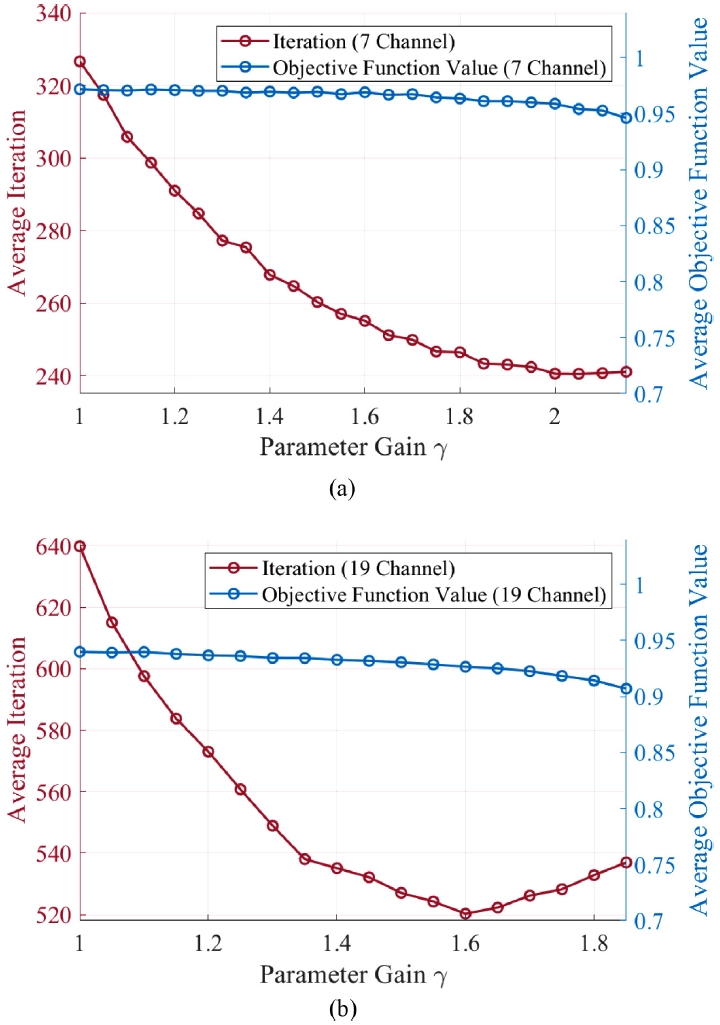
Fig. 5는
γ를 0.05씩 변화시킴에 따른 알고리즘 성능의 변화를 나타낸다. 이득 상수
γ가 1인 경우, 목적함수 변화에 따른 파라미터 값의 조정이 이루어지지 않으므로 기존의 SPGD 알고리즘과 동일한 동작을 수행한다. 이때의 평균 목적함수 값은
Fig. 4의 동작 예시와 비교하여 더 작은데, 독립 시뮬레이션 중 모든 채널의 빔이 결합하지 못하는 경우가 포함되어 있기 때문이다. 이후 7채널 및 19채널 환경 모두에서 이득 상수 값이 증가할수록 평균 반복 횟수가 감소하는 성능 향상이 일어남과 동시에 90% 이상의 결합 효율을 유지함을 확인할 수 있다.
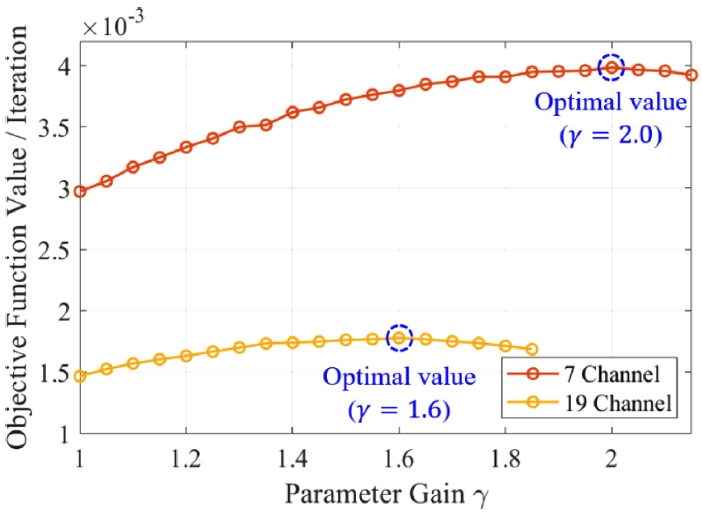
본 연구에서는
Fig. 6에서 나타난 바와 같이, 이득 상수 변화에 따른 알고리즘 성능을 보다 종합적으로 평가하기 위해 평균 목적함수 값을 평균 반복 횟수로 나눈 성능 지표를 활용하였다. 그 결과, 7채널 환경에서는
γ = 2.0일 때 최적의 성능을 나타내었으며, 19채널 환경에서는
γ = 1.6에서 가장 우수한 성능을 보였다. 이때 최적 값에서 기울기가 완만한 성능 극대 값을 가짐을 통해
γ 값의 변화에 따른 성능 민감도가 크지 않음을 확인할 수 있다.
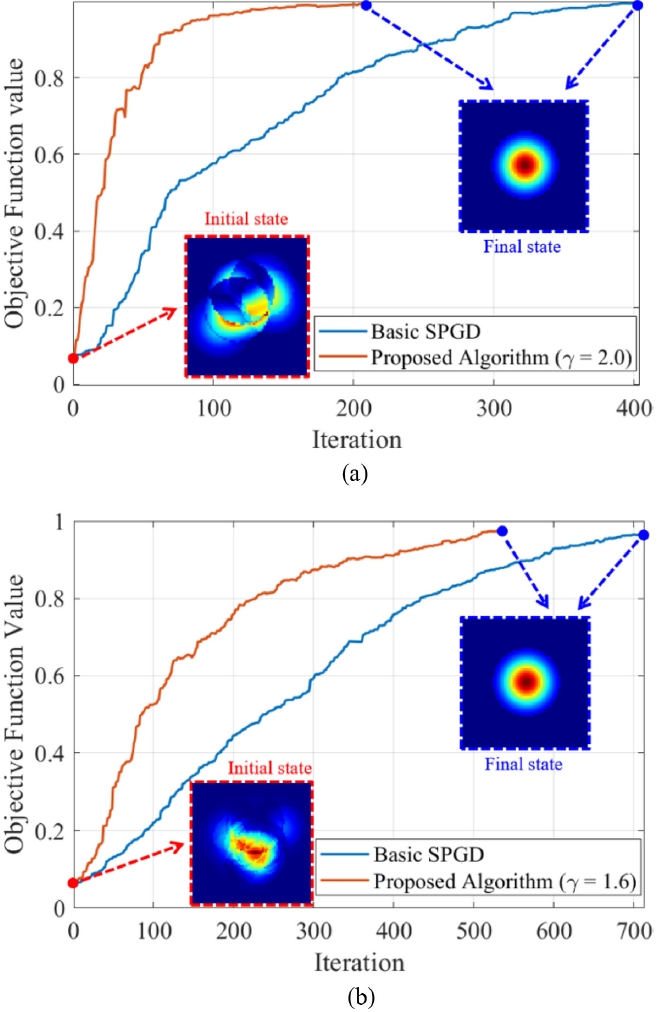
Fig. 7은 7채널과 19 채널 환경에서 기존 SPGD 알고리즘과 최적의 파라미터 이득 상수를 적용한 적응형 SPGD 알고리즘의 동작 성능을 비교한 예시를 나타낸다. 기존 SPGD 알고리즘의 경우, 시뮬레이션이 진행됨에 따라 파라미터 값이 고정되어 변경되지 않는다. 이에 따라, 알고리즘의 안정적인 수렴을 보장하기 위해서는 후반부에서 적절한 제어가 이루어질 수 있도록 파라미터의 크기를 상대적으로 작게 설정해야 한다. 그러나 이로 인해 초기 단계에서의 제어입력 크기가 불필요하게 제한되며, 결과적으로 목적함수 값을 보다 빠르게 증가시킬 수 있는 여지가 있음에도 불구하고 수렴 속도가 저하되는 문제가 발생한다.
이러한 한계로 인해, 기존 SPGD 알고리즘은 비교적 많은 반복 횟수를 요구하게 된다. 반면, 제안된 적응형 SPGD 알고리즘은 최적화된 파라미터 이득 상수와 현재 목적함수 값을 활용하여 초기 단계에서 파라미터 크기를 증가시키는 효과를 부여함으로써, 보다 빠른 수렴을 유도한다. 예를 들어
Fig. 7의 7채널 경우에서 확인할 수 있듯이, 초기 상태에서 목적함수 값이 0.07인 경우, 적응형 SPGD 알고리즘의 파라미터 크기는 약 2
1-0.07≈1.91배로 증가하여 목적함수의 빠른 증가를 유도하고, 목적함수 값이 증가함에 따라 이득 상수가 점진적으로 감소하여 후반부에서는 1로 수렴한다. 이를 통해, 적응형 SPGD 알고리즘은 초기 단계에서 보다 적극적인 제어 입력을 적용하면서도, 후반부에는 안정적인 수렴을 보장할 수 있도록 설계되었음을 확인할 수 있다.
Table 1은 임의의 초기 상태에서 제안된 적응형 SPGD 알고리즘과 기존 SPGD 알고리즘의 동작 성능을 비교한 시뮬레이션 결과를 나타낸다. 채널별 초기 위상은 임의의 위상을 가지도록 설정되었고, 초기 위치는 빔 직경 이하의 임의로 편차를 가지도록 위치시켰다. 비교 지표로는 10,000회 독립시행에 따른 평균 반복 횟수(Average Iteration), 평균 목적함수 수렴 값(Mean Convergence), 그리고 반복당 평균 연산 시간(Time per Iteration)이 포함되었다.
먼저, 평균 반복 횟수를 살펴보면, 7채널 환경에서 기존 SPGD 알고리즘은 평균 326.6회의 반복을 수행한 반면, 적응형 SPGD 알고리즘을 적용한 경우 240.5회로 감소하여 약 26.4%의 개선 효과를 보였다. 19채널 환경에서도 유사한 경향이 나타나며, 기존 SPGD 알고리즘에서 639.8회의 반복이 필요했던 것과 비교하여, 적응형 SPGD 알고리즘을 적용한 경우 524.3회로 줄어들어 18.1%의 감소 효과를 확인할 수 있다. 이를 통해 제안된 알고리즘이 초기 단계에서 보다 큰 제어 입력을 적용함으로써 목적함수 값이 빠르게 증가하도록 유도하여 전체적인 반복 횟수를 줄이는 데 기여했음을 알 수 있다.
평균 목적함수 수렴 값을 분석한 결과, 적응형 SPGD 알고리즘을 적용한 경우 기존 SPGD 알고리즘 대비 다소 낮은 값을 보였다. 7채널 환경에서는 기존 알고리즘이 0.97을 기록한 반면, 적응형 알고리즘에서는 0.96로 1.0% 감소하였다. 19채널 환경에서도 기존 알고리즘의 평균 수렴 값은 0.94였으나, 적응형 SPGD 알고리즘에서는 0.93으로 1.1% 감소하였다. 이는 적응형 SPGD 알고리즘이 초기 단계에서 큰 제어 입력을 사용함에 따라 일부 시뮬레이션 사례에서 빔의 이탈이 발생하여 다소 낮은 수렴 값을 가질 가능성이 있음을 시사한다. 여기서 빔의 이탈이란 일부 빔의 초기 위상이 주변 빔들과 반대 위상을 가질 때, 알고리즘의 학습 과정에서 목표 위치로부터 점차 벗어나는 현상을 의미한다. 그러나 이로 인한 수렴 값의 차이는 1% 내외로 속도 개선 효과에 비해 미미하며, 이에 따른 빔 품질 또한 충분히 허용 가능한 수준이다. 따라서 반복 횟수 감소에 따른 전체 수렴 효율을 고려하면, 실제 운용 측면에서의 유효 성능은 개선된 것으로 평가된다.
본 연구의 결맞음 빔결합 시뮬레이터는 MATLAB 환경에서 구축되었으며, 전체 시뮬레이션 시간은 제어를 위한 연산 시간과 시뮬레이션 환경 구성을 위한 모델링 시간을 포함한다. 7채널 환경에서는 기존 SPGD 알고리즘이 평균 0.87초, 적응형 SPGD 알고리즘이 0.68초로 21.8% 감소하였으며, 19채널 환경에서는 기존 알고리즘이 3.82초, 적응형 알고리즘이 3.22초로 15.6% 감소하였다. 이를 통해 제안된 적응형 SPGD 알고리즘 작동 과정에서 파라미터 조정을 위한 추가적인 연산이 포함되었음에도 불구하고, 전체적인 반복 횟수 감소 효과로 인해 총 연산 시간은 오히려 단축되었음을 확인할 수 있다.
5. 결론
본 연구에서는 결맞음 빔결합 시스템에서 위상 및 팁-틸트 제어 성능을 개선하기 위해 적응형 SPGD 알고리즘을 제안하였다. 기존 SPGD 알고리즘은 전체 과정에서 고정된 파라미터를 사용하기 때문에 수렴 속도가 느리고, 최적 수렴을 위해 섭동 크기 및 학습률을 보수적으로 설정해야 하는 한계를 가진다. 이를 해결하기 위해, 본 연구에서는 목적함수 값의 변화에 따라 동적으로 섭동 크기와 학습률을 실시간 조정하는 적응형 SPGD 알고리즘을 제안하고 그 성능을 시뮬레이터 환경에서 평가하였다.
제안된 알고리즘의 성능을 검증하기 위해 7채널과 19채널 환경의 시뮬레이터를 구축하고, 기존 SPGD 알고리즘과 비교 분석을 진행하였다. 시뮬레이션 결과, 제안된 적응형 SPGD 알고리즘은 기존 알고리즘 대비 평균 반복 횟수를 7채널 환경에서는 26.4%, 19채널 환경에서는 18.1% 감소시키며 빠른 수렴 성능을 보이면서도 결맞음 빔결합에 충분한 90% 이상의 결합 효율을 보였다. 적응형 파라미터 연산에 의해 반복당 연산 시간은 적응형 SPGD 알고리즘에서 소폭 증가하였으나, 전체 반복 횟수의 감소 효과를 고려하면 총 연산 시간은 감소하여 실질적인 제어 성능 개선이 이루어졌음을 확인하였다. 결과적으로, 제안된 알고리즘의 적용을 통해 채널 수 증가에 따른 기존 SPGD의 제어 대역폭 감소 문제를 보완할 수 있으며, 우수한 채널 확장성을 바탕으로 고출력 빔결합에 효과적으로 적용될 수 있을 것으로 기대된다.
본 연구에서 제안한 적응형 SPGD 알고리즘은 기존 SPGD 알고리즘에서 활용된 파라미터에서 하나의 제어 파라미터만을 추가함으로써 간단한 1차원 최적화만으로 결맞음 빔결합 시스템의 위상 및 팁-틸트 제어에서 빠르고 효율적인 수렴을 가능하게 하며, 다채널 환경에서도 적용이 가능하다. 향후 연구에서는 위상 변조기와 팁-틸트 액추에이터의 동특성과 제어 속도 차이가 반영되고 대기 터뷸런스와 같은 외란이 포함된 실제적인 결 맞음 빔결합 시뮬레이션 환경에서 적응형 파라미터의 업데이트 빈도를 조절하여 속도와 안정성 모두를 개선하는 후속 연구를 계획 중이다.
FOOTNOTES
-
ACKNOWLEDGEMENT
본 연구는 LIG Nex1 산학협력과제의 지원을 받아 수행된 연구임.
Fig. 1Schematic diagram of coherent beam combining system
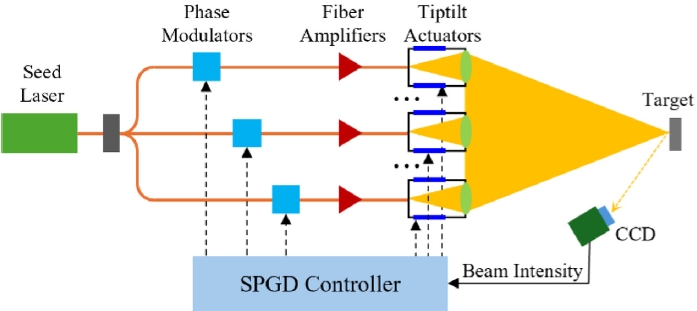
Fig. 2Schematic illustration of (a) conventional SPGD algorithm and (b) proposed adaptive SPGD algorithm
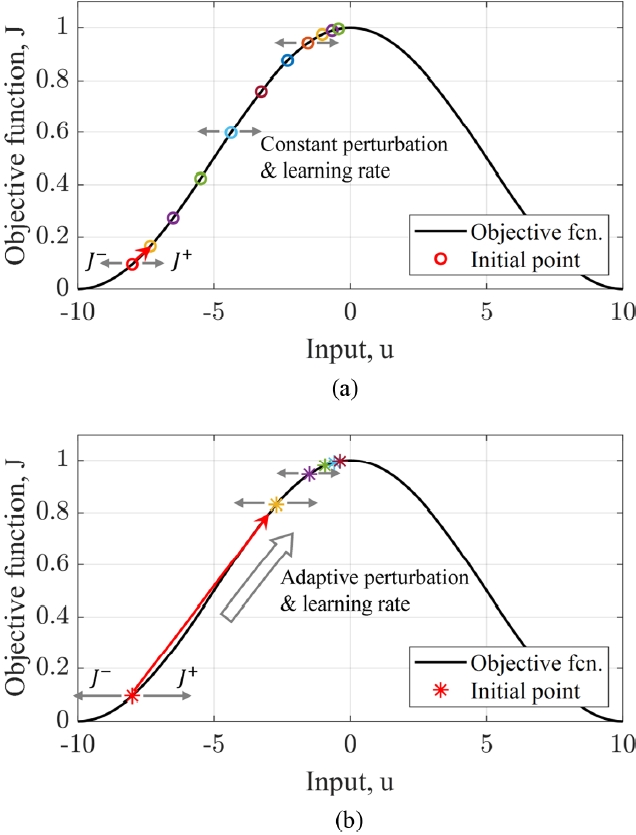
Fig. 3Three cases of 3 channel light intensity distribution with different phases and tip-tilt positions. (a) 3 channel light intensity distribution – no overlap of beams, (b) 3 channel light intensity distribution – overalapped at (0,0) with random phases, (c) 3 channel light intensity distribution – overlapped at (0,0) with phase locked
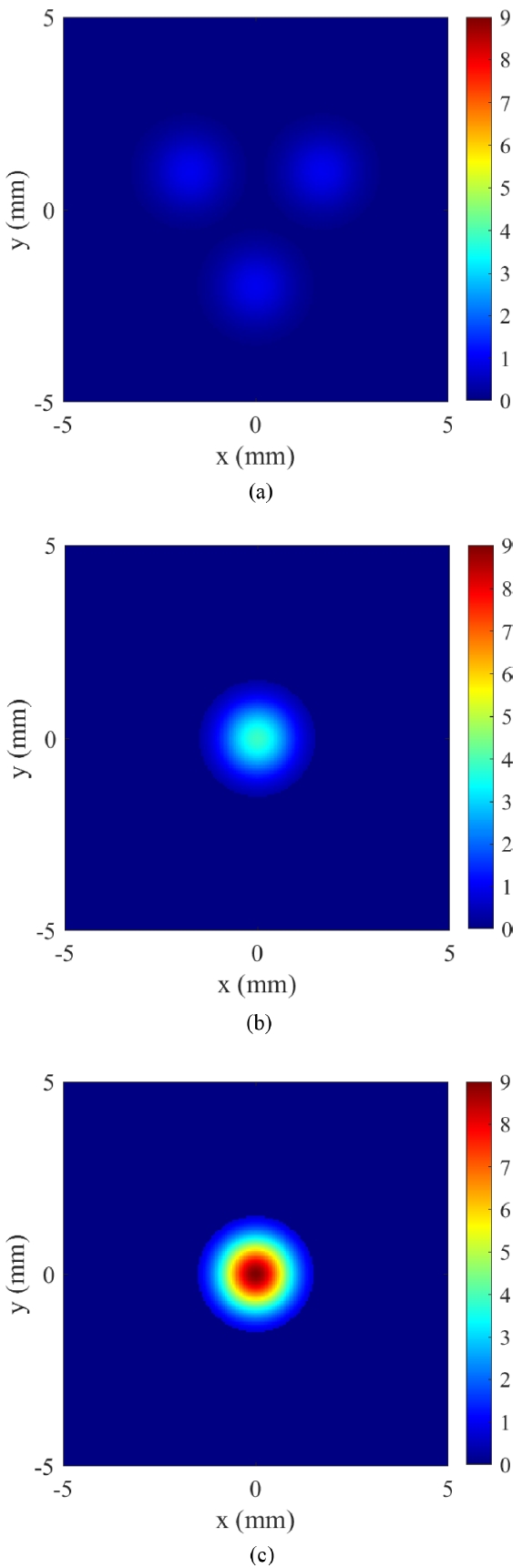
Fig. 4Simulation results for coherent beam combining systems using basic SPGD algorithm with different channel numbers
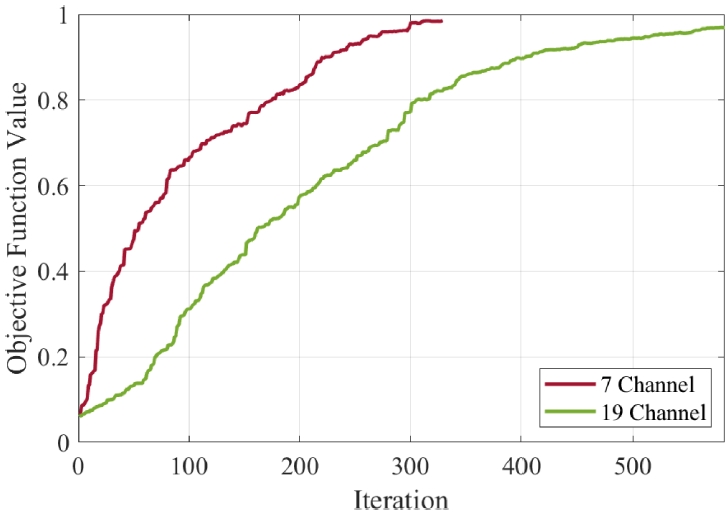
Fig. 5Coherent beam combining simulation performance evaluation of the proposed adaptive SPGD algorithm with different parameter gain values. (a) 7 channel performance, and (b) 19 channel performance
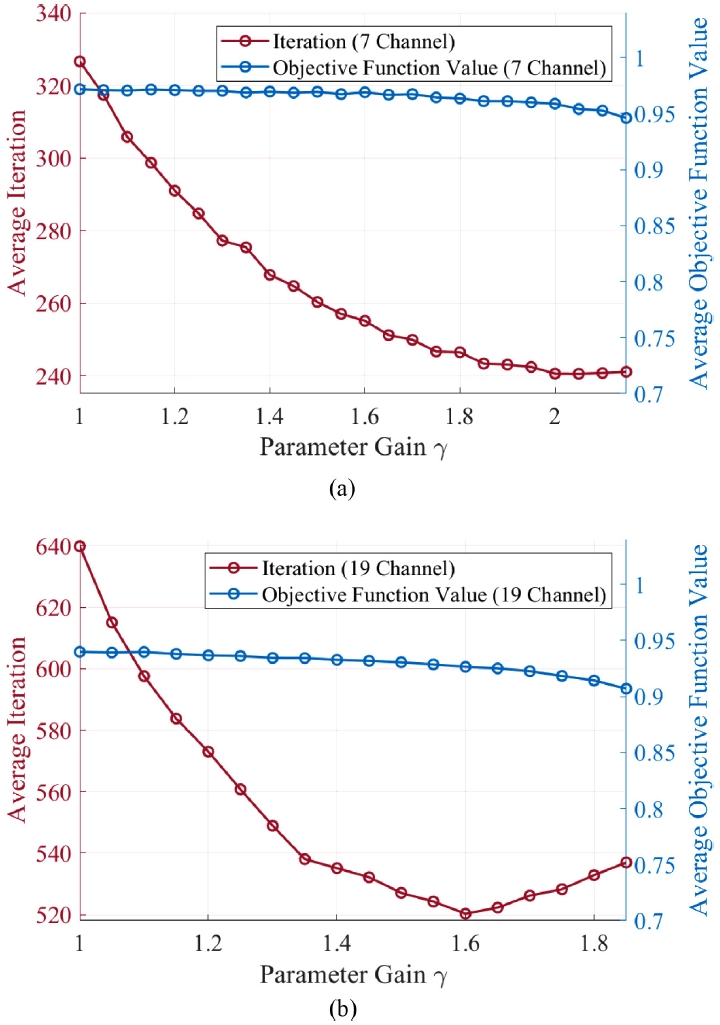
Fig. 6Parameter gain sweep results of the proposed adaptive SPGD algorithm with different channel numbers
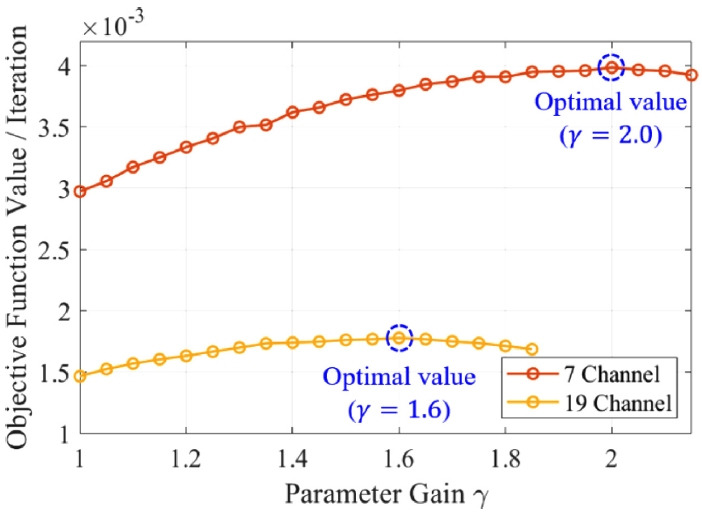
Fig. 7Simulation results of the proposed adaptive SPGD algorithm compared to the basic SPGD algorithm with different channel numbers. (a) 7 channel simulation, (b) 19 channel simulation
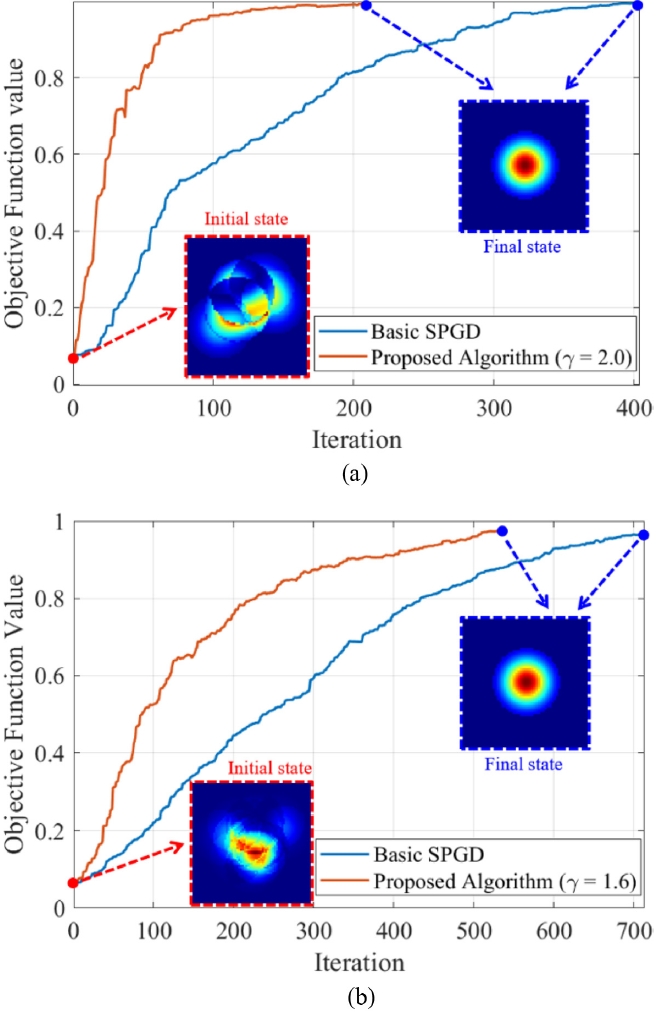
Table 1Coherent beam combining simulation results of the proposed adaptive SPGD algorithm compared to basic SPGD algorithm
Table 1
|
Channel Number |
7 |
19 |
|
Algorithm |
Basic SPGD |
Adaptive SPGD |
Change |
Basic SPGD |
Adaptive SPGD |
Change |
|
Average Iteration |
326.6 |
240.5 |
-26.4% |
639.8 |
524.3 |
-18.1% |
|
Mean Convergence |
0.97 |
0.96 |
-1.0% |
0.94 |
0.93 |
-1.1% |
|
Average Simulation Time (s) |
0.87 |
0.68 |
-21.8% |
3.82 |
3.22 |
-15.6% |
REFERENCES
- 1. Richardson, D. J., Nilsson, J., and Clarkson, W. A., (2010), High power fiber lasers: Current status and future perspectives, Journal of the Optical Society of America B, 27(11), B63-B92.
- 2. Prieto, C., Vaamonde, E., Diego-Vallejo, D., Jimenez, J., Urbach, B., Vidne, Y., and Shekel, E., (2020), Dynamic laser beam shaping for laser aluminium welding in e-mobility applications, Procedia Cirp, 94, 596-600.
- 3. Wenzel, H., Crump, P., Pietrzak, A., Wang, X., Erbert, G., and Tränkle, G., (2010), Theoretical and experimental investigations of the limits to the maximum output power of laser diodes, New Journal of Physics, 12(8), 085007.
- 4. Fathi, H., Närhi, M., and Gumenyuk, R., (2021), Towards ultimate high-power scaling: Coherent beam combining of fiber lasers, Photonics, 566.
- 5. Vorontsov, M. A., and Weyrauch, T., (2016), High-power lasers for directed-energy applications: Comment, Applied Optics, 55(35), 9950-9953.
- 6. Klenke, A., Müller, M., Stark, H., Tünnermann, A., and Limpert, J., (2018), Sequential phase locking scheme for a filled aperture intensity coherent combination of beam arrays, Optics Express, 26(9), 12072-12080.
- 7. Zuo, J., Zou, F., Zhou, X., Geng, C., Li, F., Jia, Q., Jiang, J., Li, Z., Liu, J., and Ma, X., (2022), Coherent combining of a large-scale fiber laser array over 2.1 km in turbulence based on a beam conformal projection system, Optics Letters, 47(2), 365-368.
- 8. Hu, Q., Zhen, L., Mao, Y., Zhu, S., Zhou, X., and Zhou, G., (2020), Adaptive stochastic parallel gradient descent approach for efficient fiber coupling, Optics Express, 28(9), 13141-13154.
- 9. Che, D., Li, Y., Wu, Y., Song, J., and Wang, T., (2021), Theory of admspgd algorithm in fiber laser coherent synthesis, Optics Communications, 492, 126953.
- 10. Vorontsov, M., Riker, J., Carhart, G., Rao Gudimetla, V., Beresnev, L., Weyrauch, T., and Roberts Jr, L. C., (2008), Deep turbulence effects compensation experiments with a cascaded adaptive optics system using a 3.63 m telescope, Applied Optics, 48(1), A47-A57.
- 11. Weyrauch, T., Vorontsov, M. A., Carhart, G. W., Beresnev, L. A., Rostov, A. P., Polnau, E. E., and Liu, J. J., (2011), Experimental demonstration of coherent beam combining over a 7 km propagation path, Optics Letters, 36(22), 4455-4457.
- 12. Weyrauch, T., Vorontsov, M., Mangano, J., Ovchinnikov, V., Bricker, D., Polnau, E., and Rostov, A., (2016), Deep turbulence effects mitigation with coherent combining of 21 laser beams over 7 km, Optics Letters, 41(4), 840-843.
- 13. Vorontsov, M. A., and Sivokon, V. P., (1998), Stochastic parallel-gradient-descent technique for high-resolution wave-front phasedistortion correction, Journal of the Optical Society of America A, 15(10), 2745-2758.
Biography
- Hyeong Min Yoon
received the B.S. degree in mechanical engineering in 2021 from Yonsei University, Seoul, South Korea, where he is currently working toward the Ph.D. degree in mechanical engineering. His research interest is design and precision motion control of multi degrees of freedom actuators.
- Sangmin Lee
received the B.S. degree in mechanical engineering in 2021 from Yonsei University, Seoul, South Korea, where he is currently working toward the Ph.D. degree in mechanical engineering. His research interests include electromagnetic and mechanical machine design, vibration suppression control and precision motion control for mechatronic systems.
- Jae Woo Jung
received the B.S. degree in mechanical engineering in 2020 from Yonsei University, Seoul, South Korea, where he is currently working toward the Ph.D. degree in mechanical engineering. His research interests include mechatronic systems for manufacturing, electromagnetic and electromechanical machine design, and precision motion control.
- Kang Hee Lee
received the B.S. degree in mechanical engineering in 2023 from Yonsei University, Seoul, South Korea, where he is currently working toward the Ph.D. degree in mechanical engineering. His research interests include magnetic gear, analytical modeling, and precision control.
- Jae Heon Jung
received the B.S. degree in mechanical engineering in 2024. He is currently working toward the M.S. degree in mechanical engineering at Yonsei University, Seoul, South Korea. His research interests include precision control of electromagnetic systems.
- Chang Hwan Kim
received the B.S. degree in mechanical engineering in 2024. He is currently working toward the M.S. degree in mechanical engineering at Yonsei University, Seoul, South Korea. His research interests include design and control of multi degrees of freedom 6- DOF magnetic levitation systems, precision motion control and vehicle dynamics control.
- Byunghyuck Moon
received the B.S. degree in physics from Korea University, Seoul, South Korea, in 2013 and the Ph.D. degrees in electrical engineering from Korea University, Seoul, South Korea, in 2022, respectively. He is currently a research engineer of LIG Nex1 Co.. His research interests include high power laser sources and systems for defense area.
- Eunji Park
received the Ph.D. degrees in applied physics from the Hanyang University, Seoul, South Korea, in 2009 and 2022, respectively. She is currently a research engineer of LIG Nex1 Co.. Her research interests include high p ower l aser s ources a nd s ystems for defense area.
- Ki Hyuck Kim
received the M.S. degree in control & measurement engineering from Jeonbuk University, Jeonbuk, South Korea, in 2005. He is currently a research engineer of LIG Nex1 Co.. His research interests include high power laser sources and systems for defense area.
- Seongmook Jeong
received the M.S. and Ph.D. degrees in electrical engineering and computer science from the Gwangju Institute of Science and Technology (GIST), Gwangju, South Korea, in 2009 and 2016, respectively. He is currently a research engineer of LIG Nex1 Co.. His research interests include high power laser sources and systems for defense area.
- Jun Young Yoon
received the B.S. degree in mechanical engineering from Yonsei University, Seoul, South Korea, in 2009 and the M.S. and Ph.D. degrees in mechanical engineering from the Massachusetts Institute of Technology (MIT), Cambridge, MA, USA, in 2011 and 2017, respectively.
He is currently an Associate Professor at the Department of Mechanical Engineering, Yonsei University. His research interests include manufacturing mechatronics and robotics system design, electromagnetic and electromechanical machine design, mechatronic devices for biomedical applications, and precision motion control.