ABSTRACT
This study introduces a straightforward and cost-effective method to enhance the positional accuracy of a 6-axis serial robot using a double ball-bar (DBB). Kinematic errors, a primary source of inaccuracies in offline programming, are estimated and calibrated through circular tests. The kinematics of the robot are modeled using the Denavit-Hartenberg (D-H) convention, and a mathematical relationship between radial deviation and kinematic errors is established. To avoid singularities, identifiable parameters are selected using singular value decomposition. The method involves three steps: measuring the tool center point (TCP) with the DBB, estimating key kinematic parameters, and verifying the calibration results. Redundant or less significant parameters are excluded to concentrate on the most impactful ones. During the process, the robot is commanded to trace a circular path while radial deviations are recorded. This data is then utilized to estimate and adjust the kinematic model. After recalculating and executing the circular path with the calibrated model, a notable reduction in deviation is achieved. This proposed approach requires no additional equipment and provides a quick, affordable solution for improving the accuracy of industrial robots while lowering maintenance costs.
-
KEYWORDS: Kinematic error (기구학적 오차), Kinematic parameter (기구학적 매개변수), Radial deviation (반경 편차), Double ball-bar (더블 볼바), Circular test (원호 테스트), 6-axis serial robot (6축 직렬 로봇)
NOMENCLATURE
R = Radius of a Double Ball-bar (DBB)
ΔR = Radial Deviation Measured by a DBB
ΔpTCP = TCP Position Error
Δρ = Kinematic Error of the Robot
Δρtarget = Estimated Kinematic Error
pc = Center Position of the Circular Path
p = Measured Position on the Circular Path
Tii−1
= Nominal Transformation Matrix (TM) that Defines Frame {i} Relative to the Frame {i-1}
Taii−1
= Actual TM with Kinematic Error
T6 = Nominal TM for Joint 6
T6a = Actual TM for Joint
1. 서론
산업용 로봇은 자동 제어 및 프로그래밍이 가능한 다목적 매니퓰레이터로, 조립, 용접, 이송, 도장 등 다양한 제조 공정에 활용된다[
1]. 이러한 로봇은 실린더형, 직교형, SCARA, 병렬형 등 다양한 형태로 나뉘며, 그중 다관절형 로봇은 높은 유연성과 유지보수의 용이성으로 인해 산업 현장에서 가장 널리 사용된다[
2]. 그러나 다관절형 로봇은 공작기계에 비해 위치 정확도와 구조 강건성이 낮아 고정밀 공정에는 적합하지 않다. 이러한 문제는 가공, 측정, 조립 오차 등에서 비롯되는 기하학적 오차와 백래쉬, 링크의 휨, 마모 등 비기하학적 요인으로 인해 로봇의 기구학적 모델과 실제 동작 간 불일치가 발생하기 때문이다[
3,
4]. 수동 교시 기반 시스템에서는 반복 정밀도만으로도 충분한 경우가 많지만, 최근 생산 공정의 복잡화로 인해 교시점의 수가 증가하면서 시간과 인력 소모가 커지는 문제가 있다. 이에 따라 CAD 데이터를 기반으로 한 오프라인 프로그래밍 방식이 주목받고 있으며, 이는 절대 위치 정확도까지 확보해야 하므로 정밀한 기구학적 보정이 요구된다[
5-
7].
기구학적 보정은 모델링, 측정, 파라미터 추정, 보정의 네 단계로 구성된다[
8]. 모델링은 주로 Denavit-Hartenberg (DH) 표기법을 활용하며[
9-
11], 측정은 레이저트래커, CMM, 볼바, PSD 등의 외부 측정기를 활용하여 엔드 이펙터의 위치 및 자세를 측정하는 개루프 측정방식이 많이 적용된다[
12-
14]. 수집된 데이터를 기반으로 최소자승법을 이용한 파라미터 추정이 이루어지며[
8], 이때 직접탐색법(Direct Search Method), 경사하강법 (Gradient Decent Method), Levenberg-Marquardt법 등의 최적화 알고리즘이 사용된다[
15].
로봇의 위치 정확도는 진동, 하중, 온도 변화 등 다양한 외란으로 지속적으로 변화하므로, 주기적인 성능 평가 및 보정이 필요하다[
16]. 하지만 보정 작업은 고가의 장비와 전문 인력이 요구되며, 측정 시간 동안 공정을 중단해야 하는 부담이 있다. 따라서 성능을 간단히 평가한 후, 필요한 경우에만 보정하는 방식이 경제적이다. 기존에는 ISO 9283 표준에 따른 레이저 트래커기반 평가가 일반적으로 사용되었지만[
17], 셋업 시간, 측정 환경 민감성, 경로 제약 등의 한계가 있다. 이를 보완하기 위해 볼바를 활용한 원호 테스트가 제안되었다[
18,
19].
본 연구에서는 볼바를 이용한 원호테스트를 통해 6축 직렬 로봇의 기구학적 파라미터를 추정하고 보정함으로써 위치 정확도를 향상시키는 방법을 제안한다. DH 표기법과 특이값 분해를 통해 반경편차와 기구학 오차의 관계를 모델링하고 식별 가능한 파라미터를 도출한다. 원호테스트 실험을 수행하여 보정 전 후의 반경 편차를 비교·분석함으로써 제안한 알고리즘의 유효성을 검증한다. 본 연구의 결과는 로봇 프로그래밍 및 캘리브레이션 과정에 직접 적용 가능하며, 산업용 로봇의 정확도 향상에 기여할 수 있다.
2. 볼바 측정 기반 기구학적 파라미터 추정 알고리즘
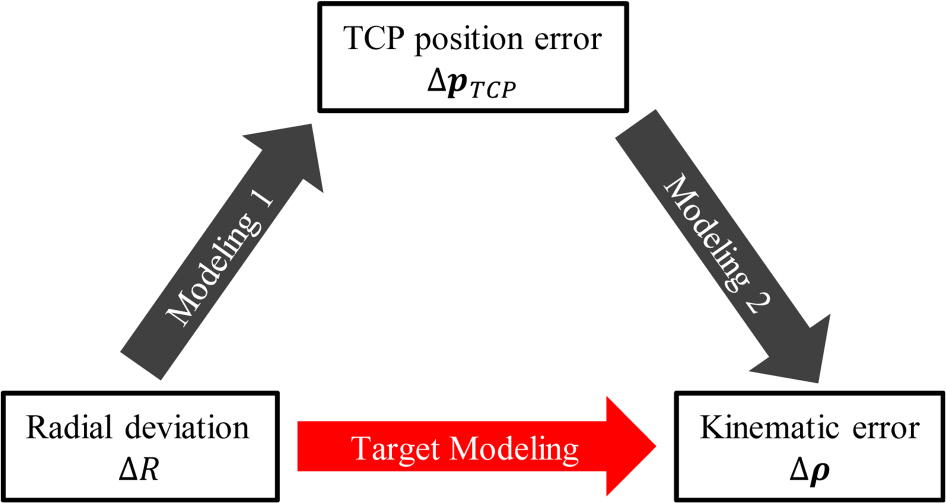
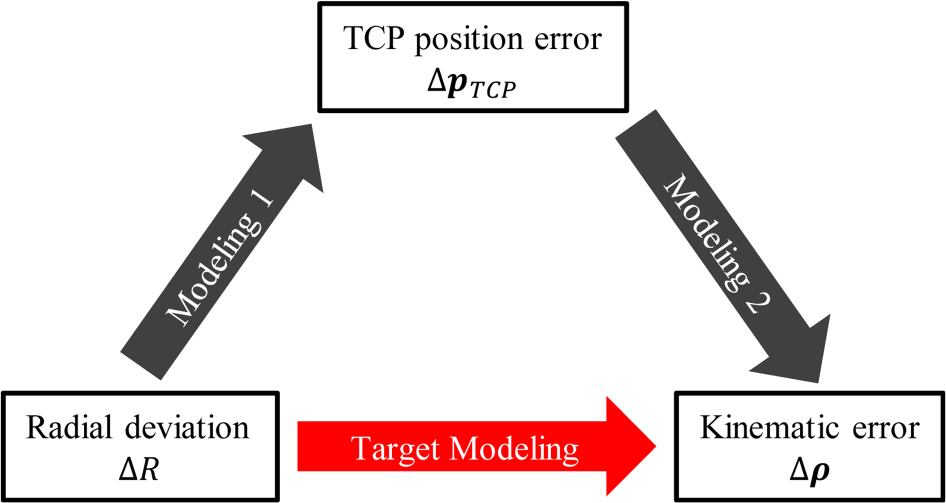
본 절에서는 볼바 측정을 활용하여 6축 직렬 로봇의 기구학적 파라미터를 추정하는 알고리즘을 설명한다. 2.1절에서는 원호테스트에서 발생하는 반경 편차와 TCP 위치 오차 간의 관계(모델1), 그리고 TCP 위치 오차와 기구학적 오차 간의 관계(모델2)를 각각 모델링 한다. 이후 두 모델을 결합하여 반경 편차와 기구학적 오차 간의 선형관계를 도출한다. 2.2절에서는 이러한 관계를 기반으로 기구학적 파라미터를 추정하는 알고리즘을 제안하며, 전체적인 알고리즘의 개요는
Fig. 1에 나타내었다.
Fig. 1An algorithm for estimating kinematic parameters from radial deviations
2.1 반경 편차 및 기구학적 오차모델링(모델1,2)
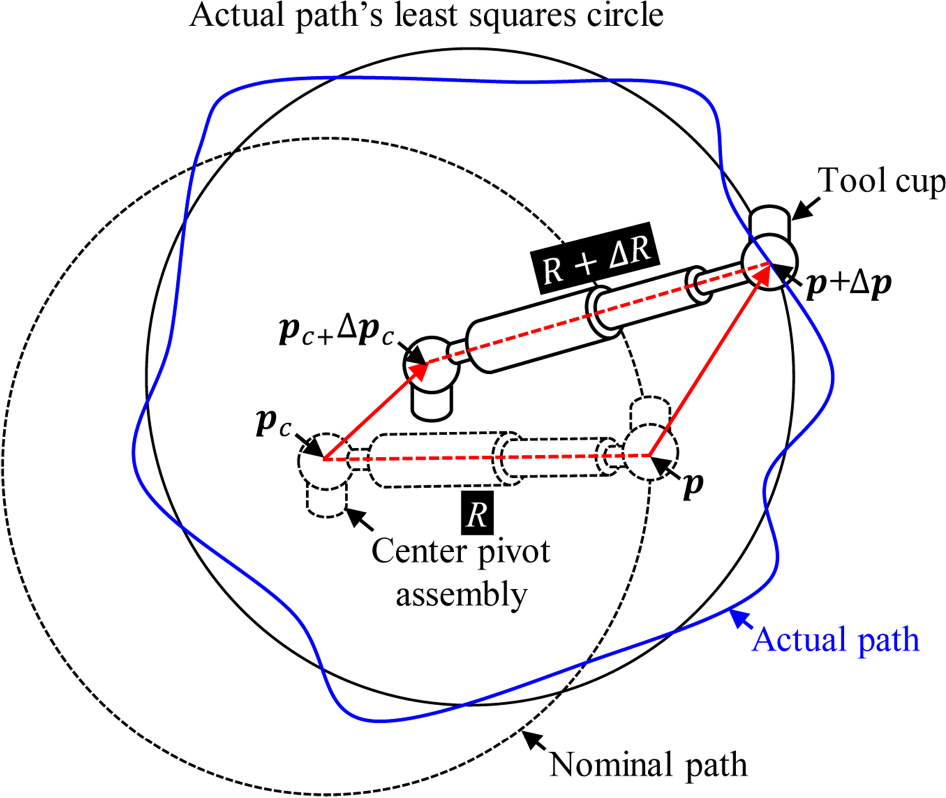
원호 테스트시 로봇의 기구학적 오차는
Fig. 2와 같이 원호 중심점
pc과 원호 상의 측정 점
p를 각각
pc +
Δpc과
p + Δp 로 변위 시키며, 이로 인해 반경 편차 ΔR이 발생한다.
Fig. 2Radial deviation induced in circular path test
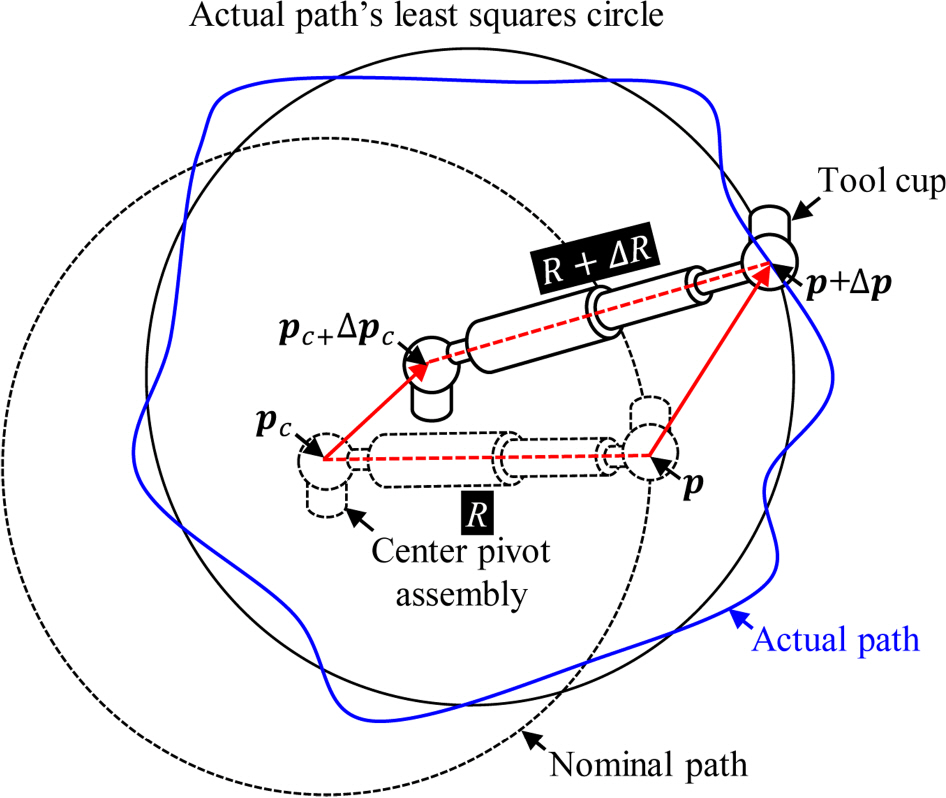
이를 수식으로 나타내면 식(1)과 같이 표현되며, 양변을 제곱한 뒤 미소하의 고차항을 제거하는 선형화 과정을 통해 반경 편차와 TCP 위치 오차 간의 관계(모델1)를 유도할 수 있고, 이는 식(2)와 같다.
링크의 기구학적 오차 모델은 {i-1}, {i}번째 링크계 사이 동종변환행렬로부터 유도한다. 기구학적 오차에 의하여 실제 변환 행렬
Taii−1
과 공칭 변환행렬
Tii−1
사이 편차
dT가 존재하며, 식(3)과 같이 나타낸다[
20].
dTi 를 테일러 전개(Taylor Expansion) 하여 미소 값을 가지는 고차항을 제거하면 식(4)와 같이 각 기구학적 오차 파라미터 (Δa, Δα, Δd, Δθ)에 대한 선형 관계식을 유도할 수 있다.
6축 직렬 로봇에 대하여, 6번 관절(플랜지)의 공칭 방위 및 위치 행렬(포즈) T6 는 식(5)와 같이 계산한다. 그러나 플랜지의 실제(Actual) 포즈 행렬 T6a 는 식(6)과 같이 T6 와 미소 변화량 dT6의 합이며, Ta의 순차적인 곱으로 이루어진다.
식(3)을 식(6)에 대입하면,
이때, 식(7)을 전개하고 미소한 값을 가지는 오차의 고차항을 제거함으로써 dT6 는 식(8)과 같이 나타낼 수 있다.
공구가 부착된 로봇 TCP의 위치오차 ΔpTCP는 dT6에 플랜 지계에 대한 TCP의 위치 6pTCP를 곱하고 기구학적 오차에 대해서 정리하면 식(9)와 같이 나타낼 수 있다.
결과적으로, TCP의 위치오차 Δ
pTCP 와 기구학적 오차 벡터 Δρ 간의 관계(모델2)는 식(10)과 같이 유도된다[
21].
여기서,
2.2 기구학적 파라미터 추정 알고리즘
2.1절에서 도출된 위치 오차와 기구학적 오차 간의 관계(모델 1) 와 TCP 위치 오차와 기구학적 오차 간의 관계(모델 2)를 나타내는 식(2)와 식(10)을 결합함으로써, 식(11)과 같이 최종적으로 측정점 p와 원호 중심점 pc 사이의 반경 편차 ΔR 과 기구학적 오차 Δρ간의 선형 관계행렬 U를 유도할 수 있다.
Bc는 pc에서의 행렬 B를 의미한다. 이때 행렬 U는 정사각행렬이 아니므로, 의사역행렬을 활용하여 기구학적 오차 벡터 Δρ 의 값을 계산한다. 이때, 선형 최소자승법의 반복적인 수행을 통해 잔류 오차를 감소시킴으로써 측정된 반경 편차 ΔRm에 대한 Δρ 의 피팅(Fitting) 성능을 개선할 수 있다. 따라서, 매 반복 시 추정된 Δρ 과 잔류 반경 편차를 이용해 새로운 선형 시스템을 유도하고, Δρ를 업데이트 한다. 이러한 과정은 최종적으로 ||Δρ||2의 크기가 10-5이하가 될 때까지 진행된다.
앞서 정의한 기구학적 오차 중 일부 요소는 원호 테스트시 측정되는 반경 편차에 영향을 미치지 않으며. 이는 행렬
U가 완전한 랭크(Full-rank)가 아니라는 점으로부터 확인할 수 있다. 랭크가 결여된(Rank-deficient) 행렬의 경우 역행렬의 신뢰성이 떨어지므로
U에서 잉여 및 의존적 열을 제거함으로써 완전한 랭크로 만드는 과정이 필수적이다. 이러한 과정은 주로 특이값 분해를 통해 이루어진다[
22]. 특이값 분해는 식(12)와 같이 대상 행렬을 두 개의 직교행렬
M,V 과 한개의 대각행렬 Σ 로 분해 하는 것으로, 이 중 Σ 는 특이값(Singular Value, σ)으로 구성된 행렬이다. 이때, σ
max/σ
min 으로 정의되는 조건수(Condition Number)는 행렬의 수치적 안정성을 나타내는 파라미터이며, 조 건수가 클수록 입력 값의 작은 동요에도 큰 오차가 유발되는 불 안정한 시스템을 의미한다[
23].
여기서,
따라서, 식(11)의 행렬 U 를 분해하여 특이값을 확인하고 시 스템의 출력 값에 영향을 주지 않는 파라미터를 제거하였다. 이 과정으로부터 시스템에 영향을 주지 않는 오차 요소 Δd1, Δd3, Δd6 을 제거하였다. 추가적으로, 이후 서술되는 오차 추정 과정을 통해 유효한 값이 추정되지 않고 발산하는 파라미터 Δd2 를 제거하였다. 각 관절 축의 오프셋 Δθ1 - Δθ6 또한 추정 대상으로부터 제외하였는데, 이는 Δθ1 - Δθ6 가 위치 의존적 (Position-dependent) 파라미터인데 반하여 원호 테스트는 모든 관절 각도에서의 특성을 반영하지 않기 때문이다. 따라서 Δθ1 - Δθ6 추정은 측정 영역 외에서 오히려 큰 오차를 야기할 수 있기 때문에, 사전에 로봇의 작업 영역이 지정되지 않는 경우 추정 대상에서 제외하는 것이 합리적이다. 결과적으로, 목표 추정기구학적 오차는 식(13)과 같다.
3. 볼바 측정 실험 및 추정 알고리즘 검증
3.1 실험 장비
제안한 방법은 산업 현장에서 사용 중인 6축 직렬 로봇(KR 60 HA, KUKA)에 적용되었다. 로봇에는
Fig. 3에 나타낸 바와 같이 공구(DED적층 공정을 위한 레이저 발진기)가 장착되어 있으며, 레이저 초점 거리에 해당하는 위치에 볼바의 정밀구가 부착되도록 센터 컵(Center Cup)이 체결되었다.
Fig. 3The deployed robot (KR 60 HA, KUKA) and the attached tool

또한, 원호 중심 위치를 고정하기 위해 테이블에는 자석을 이용해 센터 피봇 어셈블리(Center Pivot Assembly)를 설치하였다. 센터 컵과 센터 피봇 어셈블리 사이의 거리는 상용 볼바 시스템 (QC-20W, Renishaw)을 통해 측정하였으며, 로봇과 볼바의 주요 제원은 각각
Tables 1과
2에 제시되어 있다.
Table 1Specification of the deployed robot
Table 1
|
Manufacturer |
KUKA (Germany) |
|
Maximum reach [mm] |
±2,033 |
|
Positional accuracy [mm] |
±0.7 |
|
Positional repeatability [mm] |
±0.05 |
|
Path accuracy (circular) [mm] |
±0.4 |
|
Path repeatability (circular) [mm] |
±0.16 |
Table 2Specification of the utilized double ball-bar
Table 2
|
Manufacturer |
Renishaw (UK) |
|
Part name |
QC20-W |
|
Accuracy [μ m] |
±(0.7+0.3%L) |
|
Resolution [μm] |
0.1 |
|
Measurable range [μm] |
±1 |
3.2 측정 실험 및 기구학적 파라미터 추정
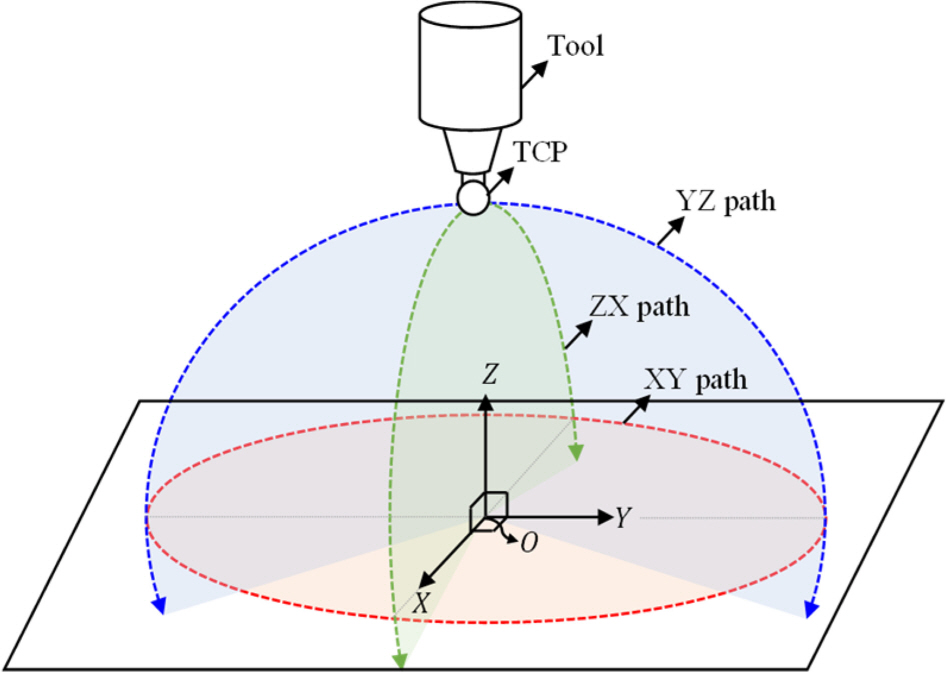
측정을 위한 원호 경로는
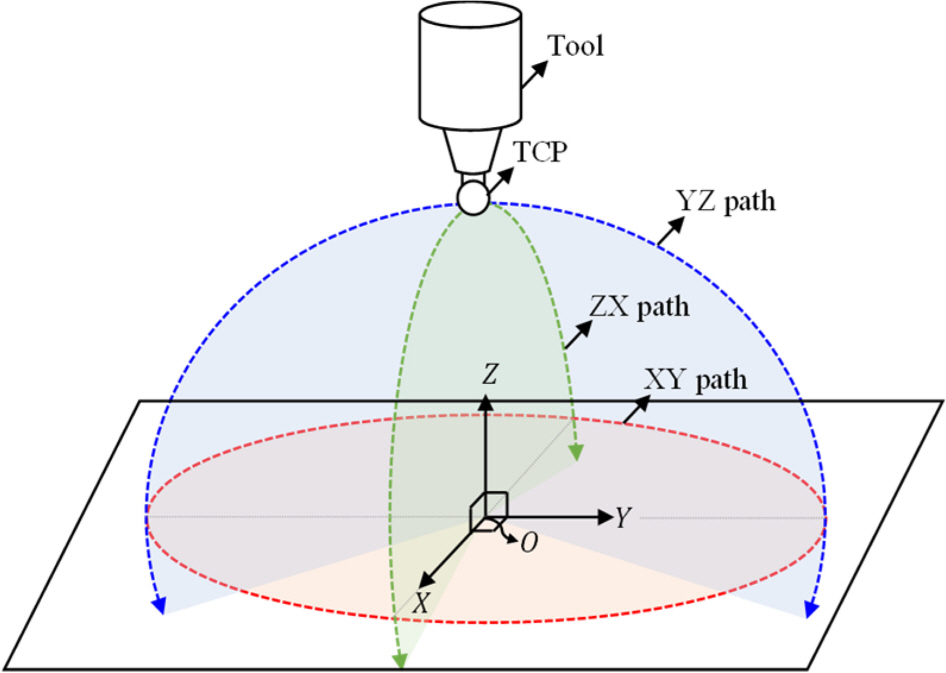
Fig. 4와 같이 로봇의 작업 공간 상의 공칭 구(Nominal Sphere) 상에 위치하고 서로 수직인 세 평면(XY, YZ, ZX) 위의 반지름 300 mm인 원호로 지정하였다. XY 평면 위에는 원형 경로를 따라 3.6°의 단위 각도로 총 100 개의 측정점을 배치하였다. 그리고 YZ, ZX 평면 상에는 사이각이 201.6°인 호에 동일한 단위 각도로 각각 57개의 측정점을 지정하였다.
Fig. 4Generated measurement paths for the circular test
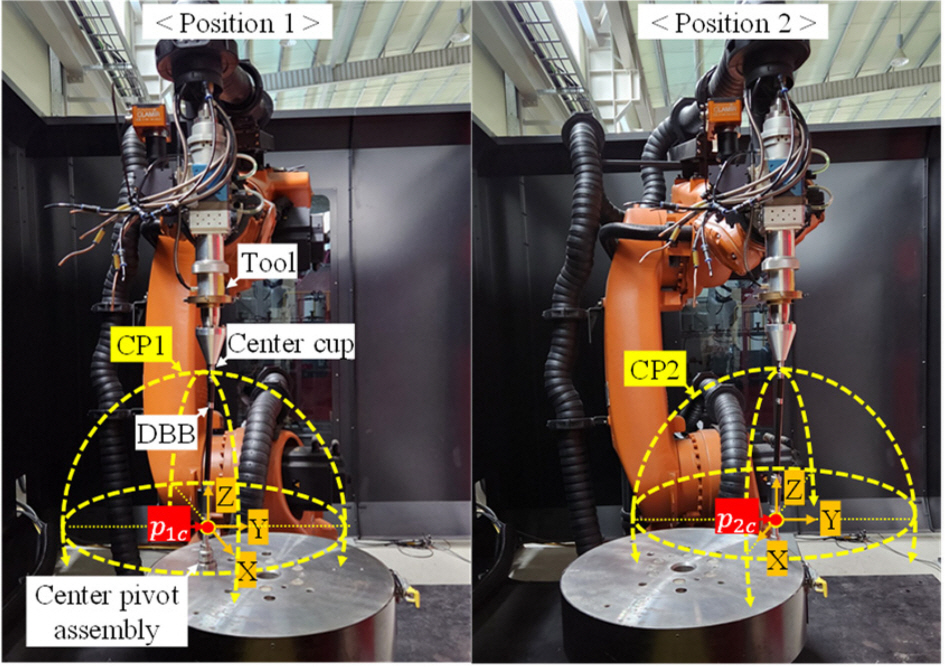
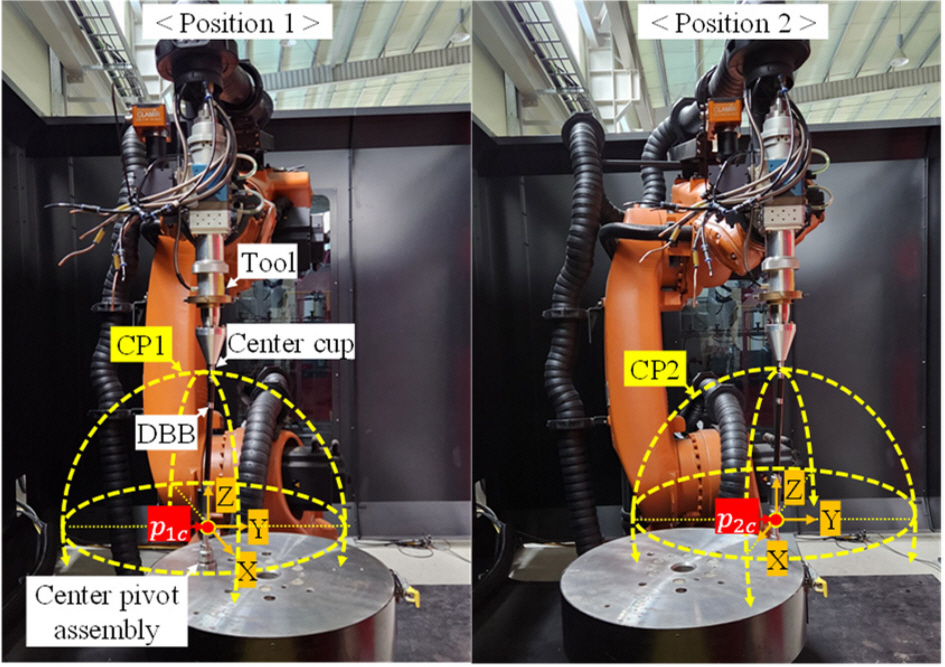
측정을 위해 중심 위치는 센터 피봇 어셈블리를 통해 고정하였다. 이후 주어진 경로로의 이송은 각 측정점에서 역기구학을 통해 사전에 계산한 관절 각도를 입력하여 제어하였다. 원호 테스트 전 공구의 끝단에 체결된 센터 컵과 센터 피봇 어셈블리에 볼바를 부착하고, 엔드 이펙터를 각 측정점으로 이송하면서 반경 편차를 기록하였다. 세 평면에 대하여 측정에 소요된 시간은 약 15분이다. 이 과정은
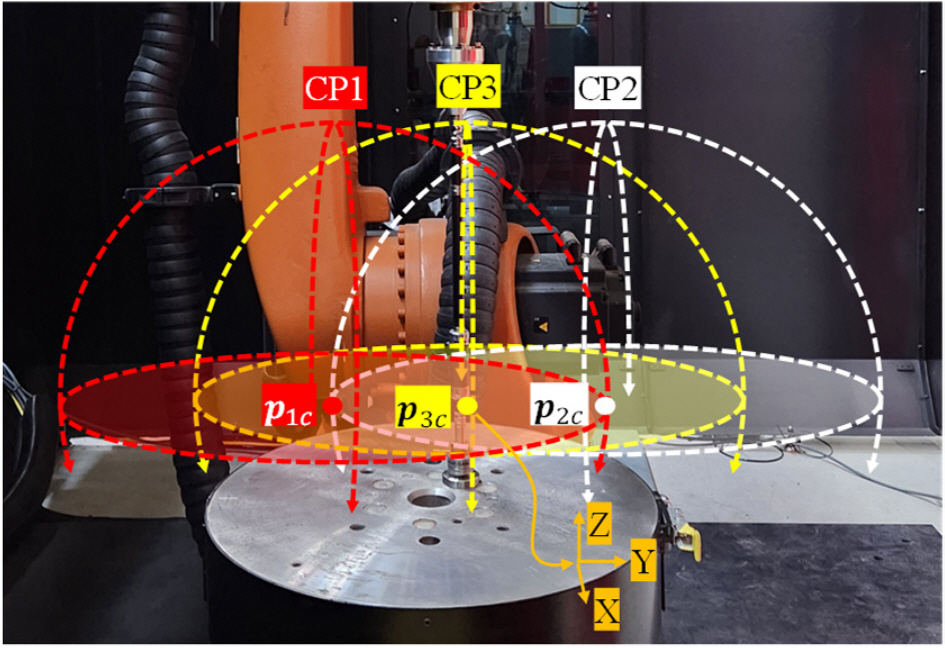
Fig. 5와 같이 로봇의 작업 영역 내 를 중심점으로 하는 두 원호 경로 CP1, CP2를 따라 진행하였다.
Fig. 5Circular paths and their center points in position 1 & 2
그 결과 총 6개의 경로, 428개의 측정 데이터(반경 편차)로부 터 제안한 알고리즘을 통해 기구학적 오차를 추정하였다. 계산은
Fig. 5의 과정이 총 4회 반복되었으며, 잔류 오차의 Norm은 8.2602에서 1.4724 mm로 감소하였다. 그 결과, 추정된 기구학적 오차의 값은
Table 3과 같다.
Table 3Estimated errors in link parameters
Table 3
|
Parameter |
Value |
|
Δa1 [mm] |
-0.9132 |
|
Δa2 [mm] |
0.5287 |
|
Δa3 [mm] |
1.2681 |
|
Δa4 [mm] |
0.1194 |
|
Δa5 [mm] |
-0.2551 |
|
Δα1 [rad] |
0.0002 |
|
Δα2 [rad] |
0.0034 |
|
Δα3 [rad] |
0.0008 |
|
Δα4 [rad] |
0.0012 |
|
Δα5 [rad] |
-0.0006 |
|
Δd4 [mm] |
0.9112 |
|
Δd5 [mm] |
-0.1850 |
3.3 추정한 기구학적 파라미터 검증
추정한 기구학적 파라미터는 로봇의 보정 기구학적 모델 fcalib 생성, 검증을 위한 원호 테스트 경로 생성 및 fcalib 의 역 기구학을 통해 각 측정점에서의 관절 각도 계산, 추정한 기구학 적 파라미터 보정 전/후 반경 편차 측정 및 비교의 순서로 검증이 이루어진다.
fcalib 은 식(14)와 같이 추정한 기구학적 오차를 로봇의 공칭 기구학적 모델 fnorm에 업데이트하여 생성한다.
검증을 위한 측정경로는 기존의 CP1과 CP2를 포함하며, 추가적으로 두 영역의 가운데에 위치하는 경로 CP3를 생성하였다. 이는 추정한 파라미터가 기존의 측정 경로와 상이한 경로에서 도 유효한지를 확인하기 위함이다. 이후 경로 CP1-CP3에 대하여,
fcalib 의 역기구학을 통해 매 측정점에서 요구되는 로봇 관절의 각도를 계산한다. 이때,
fcalib 는 분석적 역기구학을 위한 필요조건인 Euler Wrist(4-6번 관절의 회전 축이 한 점에서 교차)를 만족하지 않으므로 수치적 접근을 통한 방법이 요구된다 [
24]. 수치적 방법으로 역기구학을 하기 위해서는 목표 각도에 근접한 초기 각도가 요구되며, 이는 분석적 방법으로 계산한 각 관절의 각도로 지정하였다. 수치적 방법은 초기 로봇 엔드 이펙터의 포즈 행렬
Ti 과 목표 행렬
Tt로부터 잔류 벡터(Residual Vector)
e→ 를 유도하여 이루어지며,
e→ 는 식(16) 및 식(17)과 같이 정의된다. 목표 관절각도는 식(18)과 같이 정의한 목적함수 S를 최소화시키는 각도와 같다. 본 논문에서는 S의 값이 기준값 (10
-5) 이하가 될 때까지 θ를 업데이트하여 계산한다. 이때, 목적함수 값의 감소를 위한 최적화 알고리즘으로 Levenberg-Marquardt (LM) 방법을 이용한다. LM 방법은 Gauss-Newton법 의 수정된 형태로 자코비안을 이용한 의사역행렬에 완충 행렬 λ
i을 추가하는 것이며, λ는 완충 파라미터로써 매 단계에서 목적함수
S 의 값의 증감에 따라 증가 또는 감소한다[
25,
26].
Fig. 6Measurement paths for verification and their center points
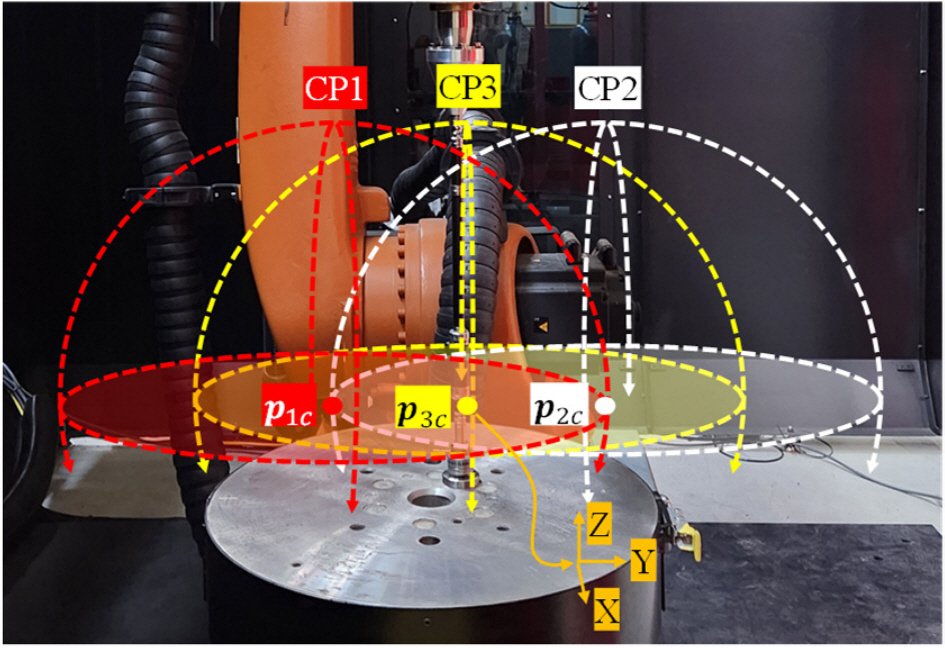
이전 단계에 비하여 목적함수의 값이 증가할 경우 λ또한 미리 지정한 곱셈계수
n 배 증가시킨다. 이때
n 이 증가할 수록 알고리즘은 경사하강법(Gradient-descent Method)의 특성에 가까워지며, 수렴에 대한 강건성이 증대되지만 수렴 속도는 감소 한다. 반대로 목적함수의 값이 감소하면 λ 가
n 배 감소되며, Newton-Raphson법의 특성에 가까워지며 수렴의 속도가 증대되지만 수렴에 대한 강건성이 감소한다[
26]. 계산을 위해 초기 λ 의 값은 0.01,
n 은 10으로 설정하였다. 예를 들어,
Fig. 5의
p1c 대하여 보정된 기구학적 모델의 역기구학을 수행하면
Table 4의 과정을 통해 목표 관절 각도가 계산된다.
Table 4Convergence of joint angles in numerical inverse kinematics at p1C
Table 4
|
Angle (deg) |
Step 1 |
Step 2 |
Step 3 |
|
Joint value |
Δ |
Joint value |
Δ |
Joint value |
Δ |
|
θ1
|
6.7440 |
0.1533 |
6.8973 |
0.0002 |
6.8975 |
0.0000 |
|
θ2
|
-94.3426 |
-0.0144 |
-94.3570 |
0.0001 |
-94.3569 |
0.0000 |
|
θ3
|
132.3457 |
0.0772 |
132.4229 |
0.000 |
132.4229 |
0.0000 |
|
θ4
|
10.8680 |
-0.1694 |
10.6986 |
0.0010 |
10.6996 |
0.0000 |
|
θ5
|
-38.4947 |
-0.0202 |
-38.5149 |
-0.0270 |
-38.5419 |
0.0000 |
|
θ6
|
-8.5278 |
0.2086 |
-8.3192 |
-0.0011 |
-8.3203 |
0.0000 |
|
S [mm2] |
4.697088 |
0.000014 |
0.000000 |
|
λ |
0.01 |
0.001 |
0.0001 |
Table 5Center positions with respect to the base coordinate system
Table 5
|
Path |
Center positions [mm] |
|
pc,x
|
pc,y
|
pc,z
|
|
CP1 |
1270.016 |
179.928 |
947.831 |
|
CP2 |
1269.937 |
-119.917 |
947.784 |
|
CP3 |
1270.003 |
29.983 |
947.921 |
각 측정점으로의 이송은 보정된 기구학적 모델 fcalib의 역기구학을 통해 계산된 관절 각도를 로봇 제어기에 입력하여 수행 하였으며, 측정 방식은 3.2절에서 기술한 방법과 동일하게 적용하였다.
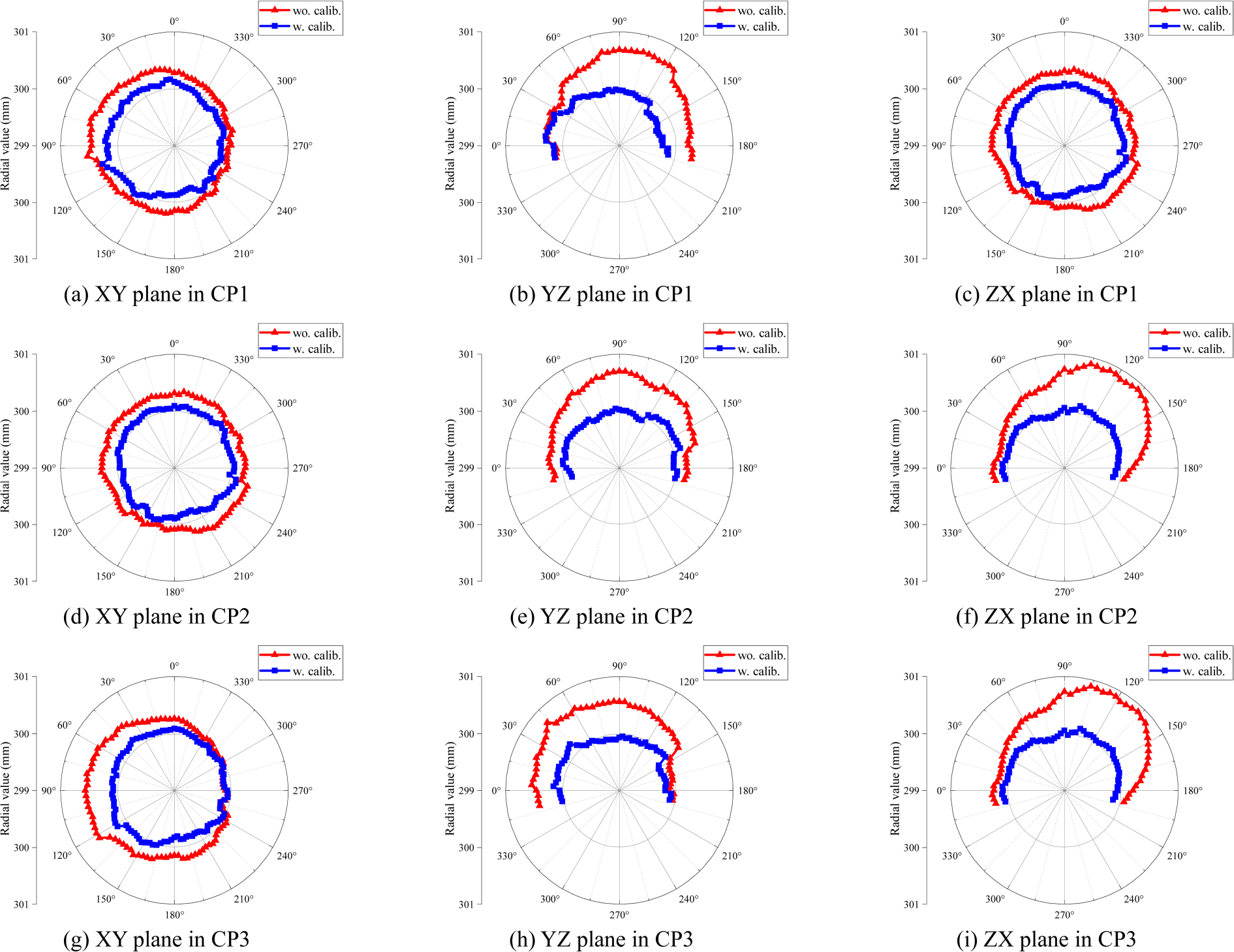
보정 전후의 경로 CP1, CP2, CP3에 대해 측정된 반경 편차 결과는
Fig. 7과
Table 6에 제시하였으며, 제안한 알고리즘을 통해 추정된 기구학적 파라미터를 적용하였을 때 측정된 반경 편차가 보정 이전에 비해 크게 감소한 것을 보여준다.
Fig. 7Measured radial deviation without / with calibration
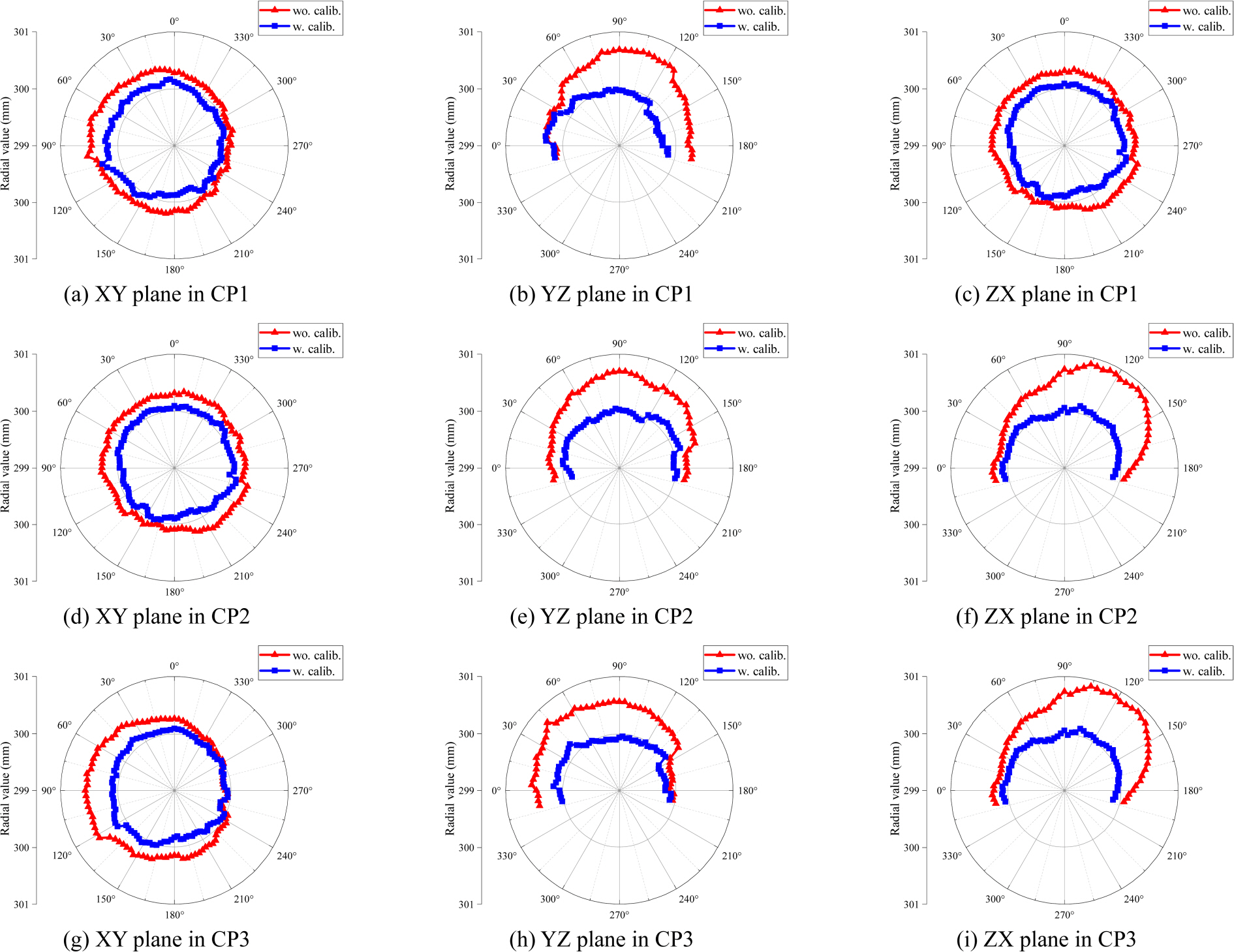
Table 6Summary of the measurement results without / with calibration
Table 6
|
Path |
Plane |
Without calibration |
With calibration |
|
Average|ΔR| [mm] |
Standard [mm] deviation |
Average|ΔR| [mm] |
Standard deviation [mm] |
|
CP1 |
XY |
0.2168 |
0.1126 |
0.1255 |
0.0566 |
|
YZ |
0.4166 |
0.1754 |
0.1450 |
0.0938 |
|
ZX |
0.4769 |
0.2466 |
0.0627 |
0.0499 |
|
CP2 |
XY |
0.2166 |
0.0600 |
0.0680 |
0.0420 |
|
YZ |
0.4280 |
0.1775 |
0.0497 |
0.0451 |
|
ZX |
0.4810 |
0.2621 |
0.0539 |
0.0301 |
|
CP3 |
XY |
0.2547 |
0.1789 |
0.0877 |
0.0442 |
|
YZ |
0.4461 |
0.2235 |
0.0952 |
0.0597 |
|
ZX |
0.4671 |
0.2575 |
0.0607 |
0.0476 |
먼저, 오차 추정을 위해 사용된 경로인 CP1과 CP2에서는 보정 후 반경 편차 절대값의 평균이 최대 88.79%까지 감소하였으 며, 표준편차 또한 88.51% 감소함을 통해 보정 효과의 유효성이 확인되었다.
또한, 보정에 사용되지 않은 경로인 CP3에서도 반경 편차 절대값의 평균이 최대 87.00%, 표준편차는 81.51% 감소함으로써, 보정 경로 외 영역에서도 추정된 기구학적 파라미터가 여전히 유효함을 확인할 수 있다.
보정 이후에도 일부 잔류하는 반경 편차는 보정 전과 유사한 개형을 보이며 나타났으며, 이는 본 논문에서 고려하지 않은 각 관절의 변위 오차(Δθ1 - Δθ6)에 기인한 것으로 판단된다.
종합적으로 볼 때, 제안한 기구학적 파라미터 보정 알고리즘은 실제 6축 산업용 로봇에 적용되었을 때 원호 테스트에서 반경 편차를 유의미하게 감소시켰으며, 이는 로봇의 위치 오차 개선에 효과적인 방법임을 입증한다.
4. 결론
본 논문은 산업용 로봇의 위치 정확도 향상을 목적으로, 볼바를 이용하여 기구학적 파라미터를 추정하는 방법을 제안하고, 실험을 통해 그 타당성을 검증하였다. 최종적으로 다음과 같은 결론을 도출하였다.
산업용 로봇의 위치 오차는 공칭 기구학적 모델과 실제 로봇 시스템 간의 차이에서 기인하며, 이를 주기적으로 측정하고 보정하는 과정은 정확도 유지에 필수적이다. 본 연구에서는 볼바를 이용한 원호 테스트를 통해 측정된 반경 편차와 로봇의 기구학적 오차 간의 관계를 모델링하고, 반복적인 최소자승법을 적용하여 파라미터 오차를 추정하는 방법을 제안하였다.
제안된 알고리즘은 실제 산업 현장의 6축 로봇에 적용되었으며, 보정 전후 서로 다른 위치에 설정된 세 개의 시험 영역에서 수행된 원호 테스트를 통해 반경 편차가 감소하는 것을 확인함으로써 기구학적 파라미터 추정의 타당성을 입증하였다.
제시된 방법은 원호 테스트 기반으로 측정 절차 및 방법이 간단하고 신속하며, 레이저 트래커에 비해 상대적으로 저렴한 측정 장비를 사용함으로써 측정 비용을 절감할 수 있다. 이를 통해 로봇 보정에 소요되는 시간과 비용을 줄이고, 전반적인 생산성 향상에 기여할 수 있을 것으로 기대된다.
본 연구에서는 D-H 파라미터 추정 시 로봇 동작에 따라 지속적으로 변하는 변수 θ를 제외하였다. 이는 θ가 구조적·기하학적 특성을 나타내는 고정 파라미터와 달라 함께 추정할 경우 모델의 일반화 성능이 저하될 수 있으며 동작 시마다 재추정이 필요할 수 있기 때문이다. 향후 연구에서는 추정된 구조적 파라 미터를 기반으로 θ를 포함한 통합적 추정을 수행하여 시스템의 성능을 향상시킬 예정이다.
ACKNOWLEDGMENTS
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재 단의 지원을 받아 수행된 연구임(No. RS-2023-NR076978).
REFERENCES
- 1. ISO 8373, (2012), Robots and robotic devices - Vocabulary.
- 2. Petrescu, F.I.T., (2022), Advanced dynamics processes applied to an articulated robot, Processes, 10(4), 640-668.
- 3. Schneider, U., Drust, M., Ansaloni, M., Lehmann, C., Pellicciari, M., Leali, F., Gunnink, J. W., and Verl, A., (2016), Improving robotic machining accuracy through experimental error investigation and modular compensation, International Journal of Manufacturing Technology, 85, 3-15.
- 4. Sun, T., Liu, C., Lian, B., Wang, P., and Song, Y., (2021), Calibration for precision kinematic control of an articulated serial robot, IEEE Transactions on Industrial Electronics, 68(7), 6000-6009.
- 5. Pan, Z., Polden, J., Larkin, N., van Duin, S., and Norrish, J., (2012), Recent progress on programming methods for industrial robots, Robotics and Computer-Integrated Manufacturing, 28(2), 87-94.
- 6. Roth, Z., Mooring, B., and Ravani, B., (1987), An overview of robot calibration, IEEE Journal of Robotics and Automation, 3(5), 377-385.
- 7. Elatta, A. Y., Gen, L. P., Zhi, F. L., Daoyuan, Y., and Fei, L., (2004), An overview of robot calibration, Information Technology Journal, 3(1), 74-78.
- 8. Mooring B. W., Roth Z. S., Driels M. R.. 1991. Fundamentals of calibration. John Wiley & Sons.
- 9. Denavit, J., and Hartenberg, R. S., (1955), A kinematic notation for lower-pair mechanisms based on matrices, Journal of Applied Mechanics, 22(2), 215-221.
- 10. Siciliano B., Khatib O.. 2008. Springer handbook of robotics. Springer.
- 11. Craig, J. J., (2005), Introduction to robotics: Mechanics and control, 3rd Ed., Pearson Education.
- 12. He, R., Zhao, Y., Yang, S., and Yang, S., (2010), Kinematic-parameter identification for serial-robot calibration based on poe formula, IEEE Transactions on Robotics, 26(3), 411-423.
- 13. Wu, C., (1984), A kinematic cad tool for the design and control of a robot manipulator, The International Journal of Robotics Research, 3(1), 58-67.
- 14. Hollerbach, J. M., and Wampler, C. W., (1996), The calibration index and taxonomy for robot kinematic calibration methods, The International Journal of Robotics Research, 15(6), 573-591.
- 15. Fares, F., Souifi, H., Bouslimani, Y., and Ghribi, M., (2021), Tool center point calibration method for an industrial robots based on spheres fitting method. Proceedings of the 2021 IEEE International Symposium on Robotic and Sensors Environments. 1-6.
- 16. Le Reun, A., Subrin, K., Dubois, A., and Garnier, S., (2022), Thermal drift and backlash issues for industrial robots positioning performance, Robotica, 40(9), 2933-2952.
- 17. ISO 9283, (1998), Manipulating industrial robots-performance criteria related test methods.
- 18. Slamani, M., Nubiola, A., and Bonev, I., (2012), Assessment of the positioning performance of an industrial robot, Industrial Robot: An International Journal, 39(1), 57-68.
- 19. Kuric, I., Tlach, V., Sága, M., Císar, M., and Zajačko, I., (2021), Industrial robot positioning performance measured on inclined and parallel planes by double ballbar, Applied Sciences, 11(4), 1777-1793.
- 20. Veitschegger, W., and Wu, C. H., (1986), Robot accuracy analysis based on kinematics, IEEE Journal on Robotics and Automation, 2(3), 171-179.
- 21. Zhenhua, W., Hui, X., Guodong, C., Rongchuan, S., and Sun, L., (2014), A distance error based industrial robot kinematic calibration method, Industrial robot: An International Journal, 41(5), 439-446.
- 22. Gao, G., Li, Y., Liu, F., and Han, S., (2021), Kinematic calibration of industrial robots based on distance information using a hybrid identification method, Complexity, 2021, 1-10.
- 23. Strang, G., (2006), Linear algebra and its applications, 4th Ed., Cengage Learning.
- 24. Kucuk, S., and Bingul, Z., (2014), Inverse kinematics solutions for industrial robot manipulators with offset wrists, Applied Mathematical Modelling, 38(7-8), 1983-1999.
- 25. Levenberg, K., (1944), A method for the solution of certain nonlinear problems in least squares, Quarterly of Applied Mathematics, 2(2), 164-168.
- 26. Gavin, H. P., (2024), The Levenberg-Marquardt algorithm for nonlinear least squares curve-fitting problems. Duke University. 1-23.
Biography
Heung Ki Jeon
MA.Sc. degree in the School of Mechanical Engineering, Kyungpook National University. His research interests are metrology, improving the positioning accuracy of robot and machine tool.
Sung Hwan Kweon
Research Fellow at the Digital Design & Digital Manufacturing R&D Center, Kyungpook National University. His research interests are methodology and performance evaluation of robots.
Kwang Il Lee
Professor in the School of Mechanical and Automotive Engineering, Kyungil University. His research interests are precision methodologies for machine tools, Robots and 3D printer.
Seung Han Yang
Professor in the School of Mechanical Engineering, Kyungpook National University. His research interests are intelligent manufacturing systems and CAD/CAM.